Table of contents
3. Introduction to Keras and TensorFlow
This chapter is meant to give you everything you need to start doing deep learning in practice. I’ll give you a quick presentation of Keras(https://keras.io) and TensorFlow(https://tensorflow.org), the Python-based deep learning tools that we’ll use throughout the book. You will find out how to set up a deep learning workspace, with TensorFlow, Keras and GPU support. Finally, building on top of first contact you had with Keras and TensorFlow in chapter 2, we will review the core components of neural networks and how they translate to Keras and TensorFlow APIs.
By the end of this chapter, you will be ready to move on to practical, real-world applications, which will start with chapter 4.
3.1 What’s TensorFlow?
TensorFlow is Python-based, free, open source machine learning platform, developed primarily by Google. Much like NumPy, the primary purpose of TensorFlow is to enable engineers and researchers to manipulate mathematical expressions over numerical tensors. But TensorFlow goes far beyond the scope of NumPy in the following ways:
-
It can automatically compute the gradient of any differentiable expression(as you saw in chapter 2), making it highly suitable for machine learning.
-
It can run not only on CPUs, but also on GPUs and TPUs, highly parallel hardware-accelarators.
-
Computation defined in TensorFlow can be easily distributed across many machines.
-
TensorFlow programs can be exported to other runtimes, such as C++, JavaScript (for browser based applications), or TensorFlow Lite (for applications running on moibile devices or embedded devices), etc. This makes TensorFlow applications easy to deploy in practical settings.
It’s important to keep in mind that TensorFlow is much more than a single library. It’s really a platform, home to a vast ecosystem of components, some developed by Google and some developed by third parties. For instance, there’s TF-Agents for reinforcement-learning research, TFX for industry-strength machine learning workflow management, TensorFlow serving for production deployment, and there’s the TensorFlow Hub repository of pretrained models. Together, tjese components cover a very wide range of use cases, from cutting-edge research to large-scale production applications.
Tensorflow scales fairly well: for instance, scientists from Oak Ridge National Lab have used it to train 1.1 exaFLOPS extreme weather forecasting model on the 27000 GPUs of the IBM Summit supercomputer. Likewise, Google has used TensorFlow to develop very compute-intensive deep learning applications, such as the chess-playing and Go-playing agent AlphaZero. For your own models, if you have the budget, you can realistically hope to scale to around 10 petaFLOPS on a small TPU pod or a large cluster of GPUs rented on Google Cloud or AWS. That would still be around 1% of the peak compute power of the top supercomputer in 2019!
3.2 What’s Keras?
Keras is a deep learning API for Python, built on top of TensorFlow, that provides a convenient way to define and train any kind of deep learning model. Keras was initially developed for research, with the aim of enabling fast deep learning experimentation.
Through TensorFlow, Keras can run on top of different types of hardware(see next figure) - GPU, TPU, or plain CPU - and can be seamlessly scaled to thousand of machines.
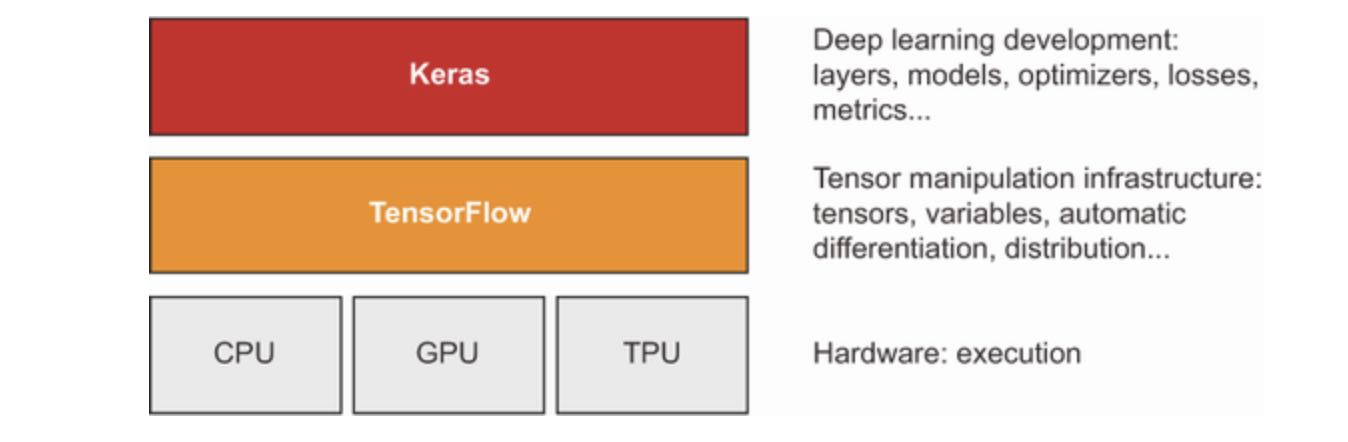
Keras is known for prioritizing the developer experience. It’s and API for human beings, not machines. It follows the best practicies for reducing cognitive load: it offers consistent and simple workflows, it minimizes the number of actions required for common use cases, and it provides clear and actionable feedback upon user error. THis makes Keras easy to learn for a beginner, and highly productive to use for an expert.
Keras has well over a million users as of late 2021, ranging from academic researchers, engineers, and data scientists at both startups and large companies to graduate students and hobbyists. Keras is used at Google, Netflix, Uber, CERN, NASA, Yelp, Instacart, Square, and hundreds of startups working on a wide range of problems across every industry. Your Youtube recommendations originate from Keras models. The Waymo self-driving cars are developed with Keras models. Keras is also a popular framework on Kaggle, the machine learning competition website where most deep learning competitions have been won using Keras.
Because Keras has a large and diverse userbase, it doesn’t force you to follow a single “true” way of building and training models. Rather, it enables a wide range of different workflows, from the very high level to the very low level, corresponding to different user profiles. For instance, you have an array of ways to build modelsand an array of ways to train them, each representing a certain trade-off between usability and flexibility. In chapter 5, we will review in detail a good fraction of this spectrum of workflows. You could be using Keras like you would use Scikit-learn - just calling fit() and letting the framework do its thing - or you could be using it like NumPy - taking control of every little detail.
This means that everything you are learning now as you are getting started will still be relevant once you become an expert. You can get started easily, and then gradually dive into the workflows where you’re writing more and more logic from scratch. You wouldn’t have to switch to an entirely different framework as you go from student to researcher, or from data scientist to deep learning engineer.
This philosophy is not unlike that of Python itself! Some languages only offer one way to write programs - for instance, object oriented programming or functional programming. Meanwhile, Python is a multiparadigm language: it offers an array of possible usage patterns that all work nicely together. This makes Python suitable to a wide range of very different use cases: system administration, data science, machine learning, web development … or just learning how to program. Likewise, you can think of Keras as the Python of deep learning: a user-friendly deep learning language offers a variety of workflows to different user profiles.
3.3 Keras and TensorFlow: a brief history
Keras predates TensoFlow by eight months. It was released in March 2015 and TensorFlow was released in November 2015. You may ask, if Keras is built on top of TensorFlow, how it could exist before TensorFlow was released? Keras was originally built on top of Theano, another tensor-manipulation library that provided automatic differentiation and GPU support - the earliest of its kind. Theano, developed at the Montreal Institute for Learning Algorithms (MILA) at the University de Montreal, was in many ways a precusrsor of TensorFLow. It pioneered the idea of using static computation graphs for automatic differentiation and for compiling code to both CPU and GPU.
In late 2015, after the release of TensorFlow, Keras was refactored to a multibackend architecture: it became possible to use Keras with either Theano or TensorFlow, and switching between the two was as easy as changing the environment variable. By September 2016, TensorFlow had reached a level of technical maturity where it became possible to make it default backend option for Keras. In 0217, two new additional backends were added to Keras: CNTK(developed by Microsoft) and MXNet(developed by Amazon). Nowadays, both Theano and CNTK are out of development, and MXNet is not widely used outside of Amazon. Keras is back to being a single-backend API - on top of TensorFlow.
Keras and TensorFlow have had a symbiotic relationship for many years. Throughout 2016 and 2017, Keras became well known as the user-friendly way to develop TensorFlow applications funneling new user into the TensorFlow ecosystem. By late 2017, a majority of TensorFlow users were using it through Keras or in combination with Keras. In 2018, the TensorFlow leadership picked Keras as TensorFlow’s official high-level API. As a result, the Keras API is front and center in TensorFlow 2.0, released in September 2019 - an extensive redesign of TensorFlow and Keras that takes into account over four years of user feedback and technical progress.
By this point, you must be eager to start running Keras and TensorFlow code in practice. Let’s get started!
3.4 Setting up a deep-learning workspace
Before you can get started developing deep learning applications, you need to set up your development environment. It’s highly recommended, although not strictly necessary, that you run deep learning on a modern NVIDIA GPU rather than your own computer’s CPU. Some applications - in particular, image processing with convolutional neural networks - will be excruciatingly slow on CPU, even a fast multicore CPU. And even for applications that can realistically be run on CPU, you will generally see the speed increase by a factor of 5 or 10 by using a recent GPU.
To do deep learning on GPU, you have three options:
- Buy and install a physical NVIDIA GPU on your workstation.
- Use GPU instance on Google Cloud or AWS EC2.
- Use the free GPU runtime from Colabarotory, a hosted notebook service offered by Google (for details about what a “notebook” is, see the next section).
Colabaratory is the easiest way to get started, as it requires no hardware purchase and no software installation - just open a tab in your browser and start coding. It’s th eoption we recommend for running the code examples in this book. However, the free version of Colabaratory is only suitable for small workloads. If you want to scale up, you’ll have to use the first or second option.
If you don’t already have a GPU that you can use for deep learning (a recent, high end NVIDIA GPU), then running deep learning experiments in the cloud is a simple low-cost way for you to move to larger workloads without having to buy any additional hardware. If you’re developing using Jupyter notebooks, the experience of running in the cloud is no different from running locally.
But if you;re a heavy user of deep learning, this setup isn’t sustainable in the long term - or even for few months. Cloud instances aren’t cheap: you’d pay $2.48 per hour for V100 GPU on Google Cloud in mid-2021. Meanwhile, a solid consumer class GPU will cost you somewhere between $1500-$2500 - a prices that has been fairly stable oer time, even as the specs of thee GPUs keep improving. If you are a heavy user of deep learning, consider setting up a local workstation with one or more GPUs.
Additionally, whether you are running locally or in the cloud, it’s better to be using a Unix workstation. Although, technically it possible to run Keras on Windows directly, we don’t recommend it. If you are a Windows user and you want to do deep learning on your own workstation, the simplest solution to get everything running is to setup an Ubuntu dual boot on your machine or to leverage Windows Subsystem for Linux (WSL), a compatibility layer that enables you to run Linux applications from Windows. It may seem like a hassle, but it will save you a lot of time and trouble in the long run.
3.4.1 Jupyter notebooks: The preferred way to run deep learning experiments
Jupyter notebooks are a great way to run deep learning experiments - in particular the many code examples in this book. They are widely used in the data science and machine learning communities. A notebook is a file generate by the Jupyter Notebook app (https://jupyter.org) that you can edit on your browser. It mixes the abilityto execute Python code with rich text-editing capabilities for annotating what you are doing. A notebook also allows you to break up long running experiments into smaller pieces that can be executed independently, which makes development interactive and means you don’t have to rerun all of your previous code if something goes wrong late in the experiment.
I recommend using Jupyter notebooks to get started with Keras, although that isn’t a requirement: you can also run standalone Python scripts or run code from within an IDE such as PyCharm. All code examples in this book are available as open source notebooks; you can download them from Github at https://github.com/fchollet/deep-learning-with-python-notebooks.
3.4.2 Using Colaboratory
Colaboratory (or colab for short) is a free Jupyter notebook service that requires no installation and runs entirely in the cloud. Effectively, it’s a web page that lets you write and execute Keras scripts right away. It gives you access to a free (but limited) GPU runtime and even a TPU runtime, so you don’t have to buy your own GPU. Colab is what we recommend for running the code examples in this book.
FIRST STEPS WITH COLAB:
To get started with Colab, go to https://colab.research.google.com and click the New Notebook button.
You will see two buttons in the toolbar: +Code and +Text. There are for creating executable Python code cells and annotation text cells, respectively. After entering code in a code cell, pressing Shift+Enter will execute the code.
Text cells are useful for giving a readable structure to your notebooks: use them to annotate your code with section title and long explanation paragraphs or to embed figures. Notebooks are meant to be a multimedia experience!
INSTALLING PACKAGES WITH PIP
The default Colab environment already comes with TensorFlow and Keras installed so you can start using it right awa without any installation steps required. But if you ever need to install something with pip, you can do so by using the following syntax in code cell (note that the line start with ! to indicated it is a shaell command rather than a Python command):
!pip install package-nameUSING THE GPU RUNTIME
To use the GPU runtime with Colab, select Runtime > Change Runtime Type in the menu and select GPU for Hardware Accelerator. Using TPU runtime with TensorFlow and Keras does require a bit of manual setup in your code. We will cover this in chapter 13.
3.5 First steps with TensorFlow
As you saw in the previous chapters, training a neural network revolves around the following concepts:
- First, low-level tensor manipulation - the infrastructure that underlies all modern machine learning. This translates to TensorFlow APIs:
- Tensors, including special tensors that store network’s state( variables).
- Tensor Operations such as addition, relu, matmul, etc.
- Backpropagation, a way to compute the gradient of mathematical expressions (handled in TensorFlow via the GradientTape object).
- Second, high level deep learning concepts. This translates to Keras APIs:
- Layers, which are combined into model.
- A loss function, which defines the feedback signal used for learning.
- An optimizer, which determines how learning proceeds.
- Metrics, to evaluate model performance, such as accuracy.
- A training loop that performs mini-batch stochastic gradient descent.
In the previous chapter you already had a first light contact with some of the corresponding TensorFlow and Keras APIs: you’ve briefly used TensorFlow’s Variable class, the matmul operation and the GradientTape. You’ve instantiated Keras Dense layers, packed them into a Sequential models, and trained that model with the fit() method.
Now let’s take a deeper dive into how all of these different concepts can be approached in practice using TensorFlow and Keras.
3.5.1 Constant tensors and variables
To do anything in TensorFlow, we are going to need some Tensors. Tensors need to be created with some initial value. For instance, you could create all-ones or all-zeros tensors, or tensors of values drawn from random distribution.
## Listing 3.1 All-ones or all-zeros tensors
>>> import tensorflow as tf
>>> x = tf.ones(shape=(2, 1)) ## Equivalent to np.ones((2, 1))
>>> print(x)
tf.Tensor(
[[1.]
[1.]], shape=(2, 1), dtype=float32)
>>> x = tf.zeros(shape=(2, 1)) ## Equivalent to np.zeros((2, 1))
>>> print(x)
tf.Tensor(
[[0.]
[0.]], shape=(2, 1), dtype=float32)## Listing 3.2 Random tensors
>>> x = tf.random.normal(shape=(3, 1), mean=0., stddev=1.) ## Tensor of random values drawn from a normal distribution with mean 0 and standard deviation 1. Equivalent to np.random.normal(size=(3, 1), loc=0., scale=1.)
>>> print(x)
tf.Tensor(
[[-0.10438307]
[ 0.72997504]
[ 0.47144324]], shape=(3, 1), dtype=float32)
>>> x = tf.random.uniform(shape=(3, 1), minval=0., maxval=1.) ## Tensor of random values drawn from a uniform distribution between 0 and 1. Equivalent to np.random.uniform(size=(3, 1), low=0., high=1.)
>>> print(x)
tf.Tensor(
[[0.88365555]
[0.77434945]
[0.7483809 ]], shape=(3, 1), dtype=float32)A significant difference between NumPy arrays and TensorFlow is that TensorFlow tensors aren’t assignable: they’re constant. For instance in NumPy, you can do the following:
## Listing 3.3 NumPy arrays are assignable
import numpy as np
x = np.ones((2, 2))
x[0, 0] = 0.Try to do the same thing in TensorFlow and you will get an error: “EagerTensor object does not support assignment”.
## Listing 3.4 TensorFlow tensors are not assignable
import tensorflow as tf
x = tf.ones((2, 2))
x[0, 0] = 0. ## This will fail as TensorFlow tensors are not assignableTo train a model, we will need to update its state, which is a set of tensors. If tensors aren’t assignables, how do we do it? That’s where variables come in. tf.Variable is the class meant to manage modifiable state in TensorFlow. You’ve already briefly seen it in action in the training loop implementation at the end of chapter 2.
To create a variable, you need to provide some initial value, such as a random tensor.
## Listing 3.5 Creating a TensorFlow variable
>>> v = tf.Variable(initial_value=tf.random.normal(shape=(3, 1)))
>>> print(v)
array([[-0.10438307],
[ 0.72997504],
[ 0.47144324]], dtype=float32)The state of a variable can be modified via its assign method, as follows:
## Listing 3.6 Assigning a value to a TensorFlow variable
>>> v.assign(tf.ones((3, 1)))
array([[1.],
[1.],
[1.]], dtype=float32)It also works for a subset of coefficients.
## Listing 3.7 Assigning a value to a subset of coefficients of a TensorFlow variable
>>> v[0, 0].assign(3.)
array([[3.],
[1.],
[1.]], dtype=float32)Similarly, assign_add and assign_sub are efficient equivalents of += and -=, respectively.
## Listing 3.8 Using assign_add()
>>> v.assign_add(tf.ones((3, 1)))
array([[4.],
[2.],
[2.]], dtype=float32)3.5.2 Tensor operations: Doing math in TensorFlow
Just like NumPy, TensorFlow offers a large collection of tensor operations to express mathematical formulas. Here are a few examples:
## Listing 3.9 A few basuc math operations in TensorFlow
a = tf.ones((2, 2))
b = tf.square(a)
c = tf.sqrt(a)
d = b + c ## Add two tensors (element-wise)
e = tf.matmul(a, b)
e *= d ## Multiply two tensors (element-wise)Importantly, each of the preceding operations gets executed on the fly: at any point you can print what the current result is, just like in NumPy. We call this eager execution.
3.5.3 A second look at the GradientTape API
So far, TensorFlow seems to look a lot like NumPy. But here’s something NumPy can’t do: retrieve the gradient of any differntialbe expression with respect to any of its inputs. Just open a GradientTape scope, apply some computation to one of the input tensors, and retrieve the gradient of the result with respect to the input.
## Listing 3.10 Using the GradientTape
input_var = tf.Variable(initial_value=3.)
with tf.GradientTape() as tape:
result = tf.square(input_var)
gradient = tape.gradient(result, input_var)This is most commonly use to retrieve the gradients of the loss of a model with respect to its weights: gradients = tape.gradient(loss, weights). You saw this in chapter 2.
So far, you’ve only seen the case where the input tensors in the tape.gradient() were TensorFlow variables. It’s actually possible for these inputs to be any arbitrary tensor. However, only trainable vaariables are tracked by default. With a constant tensor, you’d have to manually mark it as being tracked by calling tape.watch() on it.
## Listing 3.11 Using the GradientTape with constant tensor inputs
input_const = tf.constant(3.)
with tf.GradientTape() as tape:
tape.watch(input_const)
result = tf.square(input_const)
gradient = tape.gradient(result, input_const)Why is this necessary? Because it would be too expensive to preemptively store the information required to compute the gradient of anything with respect to anything. To avoid wasting resources, the tap needs to know what to watch. Trainable variables are watched by default because computing the gradient of a loss with regard to a list of trainable variables is the most common use of the gradient tape.
The gradient tape is a powerful utility, even capable of computing second-order gradients, that is to say, the gradient of a gradient. For instance, the gradient of the position of an object with regard to time is its speed of the object, and the second-order gradient is its accelartion.
If you measure the position of a falling apple along the vertical axis over time and find it verifies position(time) = 4.9 * time ** 2, what is its acceleration? Let’s use two nested gradient tapes to find out.
## Listing 3.12 Computing second-order gradients with the GradientTape
time = tf.Variable(0.)
with tf.GradientTape() as outer_tape:
with tf.GradientTape() as tape:
position = 4.9 * time ** 2
speed = tape.gradient(position, time)
acceleration = outer_tape.gradient(speed, time) ## We use the outer tape to compute the gradient of the gradient from the inner tape. Naturally the answer is 9.8, the acceleration of gravity.3.5.4 An end-to-end example: A linear classifier in pure TensorFlow
You know about tensors, variables, and tensor operations, and you know how to compute gradients. That’s enough to build any machine learning model based on gradient descent. And you are only at chapter 3!
In a machine learning job interview, you may be asked to implement a linear classifier from scratch in TensorFlow: a very simple task that serves as a filter between candidates who have some minimal machine learning background and those who don’t. Let’s get you past that filter and use your newfound knowledge of TensorFlowto implement such a linear classifier.
First let’s come up with some nicely linearly separable synthetic data to work with: two classes of points in a 2D plane. We will generate each class of points by drawing their coordinates from a random distribution with a specific covariance matrix and a specific mean. Intuitively, the covariance matrix describes the shape of the point cloud, and the mean describes its position in the plane. We will reuse the same covariance matrix for both point clouds, but we will use two different mean value - point clouds will have the same shape but different positions.
## Listing 3.13 Generating two classes of random points in the 2D plane
num_samples_per_class = 1000
negative_samples = np.random.multivariate_normal( ## Generate the first class of points: 1000 random 2D points. cov=[[1,0.5]90.5, 1] corresponds to an oval-like point cloud oriented from bottom left to top right.
mean=[0, 3],
cov=[[1, 0.5], [0.5, 1]],
size=num_samples_per_class)
positive_samples = np.random.multivariate_normal( ## Generate the other class of points with a different mean and the same covariance matrix.
mean=[3, 0],
cov=[[1, 0.5], [0.5, 1]],
size=num_samples_per_class)In the preceding code, negative_samples and positive_samples are both arrays with shape (1000, 2). Let’s stack them into a single array with shape (2000, 2)
## Listing 3.14 Stacking the two classes of points into a single array with shape (2000, 2)
inputs = np.vstack((negative_samples, positive_samples)).astype(np.float32)
Let’s generate the corresponding target labels, an array of zeros and ones of shape (2000, 1) where targets[i, 0] is 0 if inputs[i] belongs to class 0 (and inversely).
## Listing 3.15 Generating the corresponding targets (0 and 1)
targets = np.vstack((
np.zeros((num_samples_per_class, 1), dtype="float32"),
np.ones((num_samples_per_class, 1), dtype="float32"))
)Now let’s plot our data with Matplotlib.
## Listing 3.16 Plotting the two classes of points
import matplotlib.pyplot as plt
plt.scatter(inputs[:, 0], inputs[:, 1], c=targets[:, 0])
plt.show()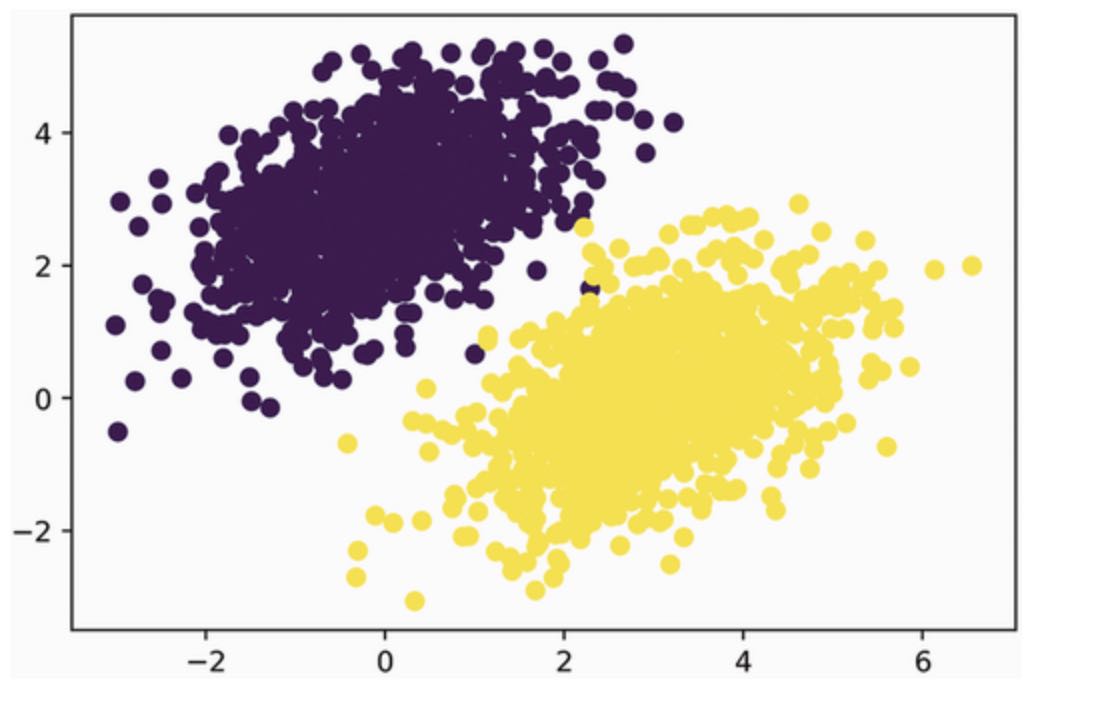
Now let’s create a linear classifier that can learn to separate these two blobs. A linear classifier is an affine transformation (prediction = W * input + b) trained to minimize the square of difference between predictions and the targets.
As you will see, it’s actually a much simpler example than the end-to-end example of two-layer neural network you saw at the end of chapter 2. However, this time you should be able to understand everything about the code, line by line.
Let’s create our variables, W and b, initialized with randome values and with zeros respectively.
## Listing 3.17 Creating the linear classifier variables
input_dim = 2 ## The input will be 2D points
output_dim = 1 ## The output predictions will be single score per sample (close to 0 if the sample is predicted to be in class 0, close to 1 if it's predicted to be in class 1)
W = tf.Variable(initial_value=tf.random.uniform(shape=(input_dim, output_dim)))
b = tf.Variable(initial_value=tf.zeros(shape=(output_dim,)))Here’s our forward pass function
## Listing 3.18 The forward pass function
def model(inputs):
return tf.matmul(inputs, W) + bBecause our linear classifier operates on 2D inputs, W is really just two scalar coefficients, w1 and w2: W = [[w1], [w2]]. Meanwhile, b is a single scalar coefficient. As such, for a given input point [x, y], its predictinon value is prediction = [[w1], [w2]] * [[x], [y]] + b = w1 * x + w2 * y + b.
The following listing shows our loss function:
## Listing 3.19 The mean squared error loss function
def square_loss(targets, predictions):
per_sample_losses = tf.square(targets - predictions) ## per_sample_losses will be a tensor with the same shape as targets and predictions, containing per-sample loss scores.
return tf.reduce_mean(per_sample_losses) ## We need to average these per-sample loss scores into a single scalar loss value: this is what reduce_mean does.Next is the training step, which receives some training data and updates the weights W and b so as to minimize the loss data.
## Listing 3.20 The training step function
learning_rate = 0.1
def training_step(inputs, targets):
with tf.GradientTape() as tape:
predictions = model(inputs) ## Forward pass inside a GradientTape scope
loss = square_loss(targets, predictions)
gradient_W, gradient_b = tape.gradient(loss, [W, b]) ## Retrieve the gradient of the loss with respect to weights.
W.assign_sub(learning_rate * gradient_W) ## Update the weights
b.assign_sub(learning_rate * gradient_b)
return lossFor simplicity, we will do batch training instead of mini-batch training. We will run each training step (gradient computation and weight update) for all the data, rather than iterate over the data in small batches. On one hand, this means that each training step will take much longer to run, since we will compute the forward pass and the gradients for 2,000 samples at once. On the other hand, each gradient update will be much more efficient at reducing the loss on the training data, since it will encompass information from all training samples instead of, say, 128 random samples. As a result, we will need mand fewer steps of training and we should use a larger learning rate than we would typically use for mini-batch training (we will use learning_rate = 0.1 defined in listing 3.20)
## Listing 3.21 The batch training loop
for step in range(40):
loss = training_step(inputs, targets)
print(f"Loss at step {step}: {loss:.4f}")After 40 steps, the training loss seems to have stablized around 0.025. Let’s plot how our linear model classifies the training data points. Because our targets are zeros and ones, a given input will be classified as “0” if its prediction value is below 0.5 and as “1” if it is above 0.5.
predictions = model(inputs)
plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5)
plt.show()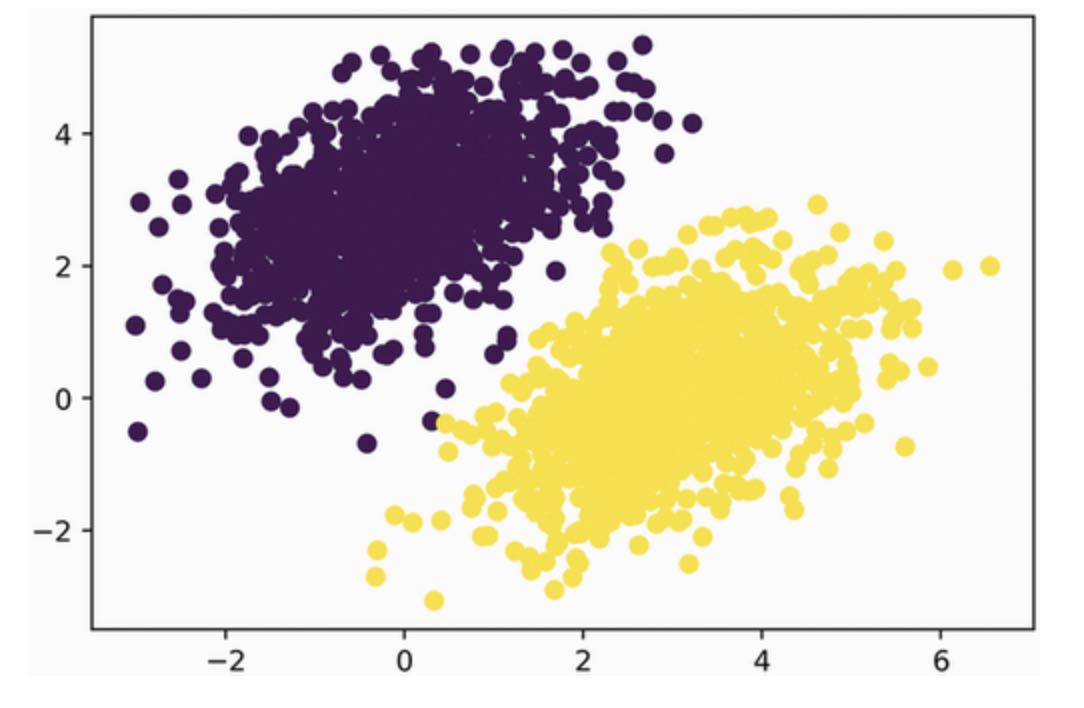
Recall that the prediction value for a given point [x, y] is simply prediction == [[w1], [w2]] * [x, y] + b == w1 * x + w2 * y + b. Thus, class 0 is defined as w1 * x + w2 * y + b < 0.5 and class 1 is defined as w1 * x + w2 * y + b > 0.5. You will notice that what you’re looking at is really the equation of a line in the 2D plane: w1 * x + w2 * y + b = 0.5. Above the line is class 1, and below the line is class 0. You may be used to seeing line equations in the format y = a * x + b in the same format, our lines becomes y = - w1 / w2 * x + (0.5 - b) / w2.
Let’s plot this line:
x = np.linspace(-1, 4, 100) ## Generate 100 regularly spaced points between -1 and 4, which we will use to plot our line
y = - W[0] / W[1] * x + (0.5 - b) / W[1] ## This is our line's equation
plt.plot(x, y, "-r")
plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5)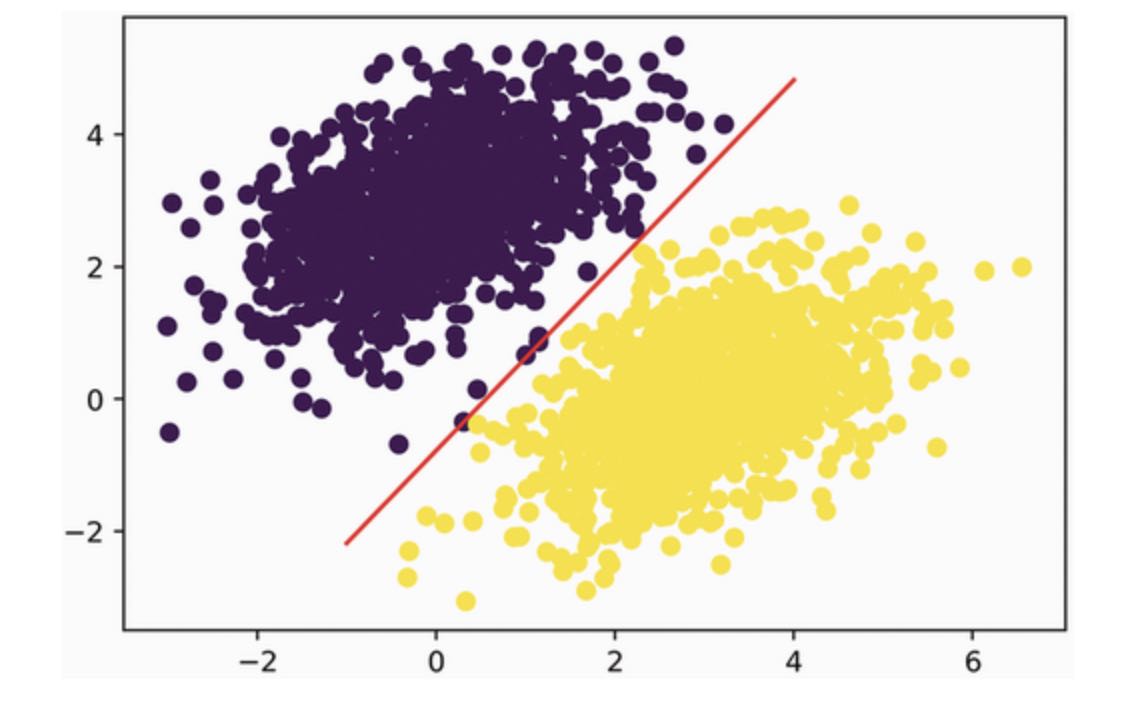
This is what a linear classifier is all about: finding the parameters of line (or higher-dimensional spaces, a hyperplane) nearly separating two classes of data.
3.6 Anatomy of a neural network
At this point you know the basics of TensorFlow, and you can use it to implement a toy model from scratch, such a the batch linear classifier in the previous section, or the toy neural network at the end of chapter 2. That’s a solid foundation to build upon. It’s now time to move on to a more productive, more robust path to deep learning: the Keras API.
3.6.1 Layers: the building blocks of deep learning
The fundamental data structure in neural networks is the layer, to which you were introduced in chapter 2. A layer is a data processing module that takes as input one or more tensors and that outputs one or more tensors. Some layers are stateless, but more frequently layers have a state: the layer’s weights, one or several tensors learned with stochastic gradient descent, which together contain the network’s knowledge.
Different types of layers are appropriate for different tensor formats and different types of data processing. For instance, simple vector data, stored in rank-2 tensors of shape (samples, features), is often processed by densely connected layers, also called fully connected or dense layers. Sequence data, stored in rank-3 tensors of shape (samples, timesteps, features), is typically processed by recurrent layers such as an LSTM layer or 1D convolution layers(Conv1D). Image data, stored in rank-4 tensors, is usually processed by 2D convolution layers (Conv2D).
You can think of layers as the LEGO bricks of deep learning, a metaphor that is made explicitly by Keras. Building deep learning models in Keras is done by clipping together compatible layers to form useful data-transformation pipelines.
THE BASE LAYER CLASS IN KERAS:
A simple API should have a single abstraction around which everything is centered. In Keras, that the Layer class. Everything in Keras is either a Layer or something that closely interacts with a Layer.
A Layer is an object that encapsulates some state (weights) and some computation (a forward pass). The weights are typically defined in a build() (although they could also be created in constructor, __init__()), and the computation is defined in the call() method.
In the previous chapter, we implemented a NaiveDense class that contained two weights W and b and applied the computation output = activation(dot(input, W) + b). This is what the same layer would looke like in Keras.
## Listing 3.22 A Dense layer implemented as a Layer subclass
from tensorflow import keras
class SimpleDense(keras.layers.Layer): ## All Keras layers inherit from the base Layer class.
def __init__(self, units, activation=None):
super().__init__()
self.units = units
self.activation = activation
def build(self, input_shape): ## Weight creation takes place in the build() method.
input_dim = input_shape[-1]
self.W = self.add_weight( ## add_weight() is a shortcut method for creating weights. It is also possible to create standalone variables and assign them as layer attributes, like self.W = tf.Variable(tf.random.uniform(w_shape)).
shape=(input_dim, self.units),
initializer="random_normal"
)
self.b = self.add_weight(
shape=(self.units,),
initializer="zeros",
)
def call(self, inputs): ## We define forward pass computation in the call() method.
y = tf.matmul(inputs, self.W) + self.b
if self.activation is not None:
y = self.activation(y)
return yIn the next section, we will cover in detail the purpose of build() and call() methods. Don’t worry if you don’t understand everything just yet!
Once instantiated, a layer like this can be used just like a function, taking as input a TensorFlow tensor:
>>> my_dense = SimpleDense(units=32, activation=tf.nn.relu) ## Instantiate our layer, defined previously.
>>> input_tensor = tf.ones(shape=(2, 784)) ## Create some test inputs.
>>> output_tensor = my_dense(input_tensor) ## Call the layer on the inputs, just like a function.
>>> print(output_tensor.shape)
(2, 32)You are probably wondering, why did we have to implement call() and build(), since we ended up using our layer plainly by calling it, that is to say, by using its __call__() method? It’s because we want to be able to create the state just in time. Let’s see how it works.
AUTOMATIC SHAPE INFERENCE: BUILDING LAYERS ON THE FLY
Just like with LEGO bricks, you can only “clip” together layers that are compatible. The notion of layer compatibility here refers specifically to the fact that every layer will only accept input tensors of a certain shape and will return output tensors of a certain shape. Consider the following example:
from tensorflow.keras import layers
layer = layers.Dense(32, activation="relu") ## A dense layer with 32 output unitsThis layer will return a tensor where the first dimension has been transformed to be 32. It can only be connected to a downstream layer that expects 32-dimensional vector as input.
When using Keras, you don’t have to worry about size compatibility most of the time, because the layers you add to your models are dynamically built to match the shape of the incoming layer. For instance, suppose you write the following:
from tensorflow.keras import models
from tensorflow.keras import layers
model = models.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(32)
])The layers didn’t receive any information about the shape of their inputs - instead they automatically inferred their input shape as being the shape of the first inputs they see.
In the toy version of the Dense layer we implemented in chapter 2 (which we named NaiveDense), we had to pass the layer’s input size explicitly to the constructor in order to be able to create its weights. That’s not ideal, because it would lead to models that look like this, where each new layer need to be made aware of the shape of the layer before it:
model = NaiveSequential([
NaiveDense(input_size=784, output_size=32, activation="relu"),
NaiveDense(input_size=32, output_size=64, activation="relu"),
NaiveDense(input_size=64, output_size=32, activation="relu"),
NaiveDense(input_size=32, output_size=10, activation="softmax"),
])It would be even worse if the rules used by a layer to produce its output shape are complex. For instance, what if our layer returned outputs of shape (batch, input_ize*2 if input_size % 2 == 0 else input_size*3)?
If we were to reimplement our NaiveDense layer as Keras layer capable of automatic shape inference, it would look like the previous SimpleDense layer (see listing 3.22), with its build() and call() methods.
In SimpleDense, we no longer create weights in the constructor like in the NaiveDense example; instead, we create them in a dedicated state-creation method, build(), which receives as an argument the first input shape seen by layer. The build() method is called automatically the first time the layer is called (via the __call__() method). In fact, that’s why we defined the computation in a separate call() method rather than in the __call__() method directly. The __call__() method of ht ebase layer schematically looks like this:
def __call__(self, inputs):
if not self.built:
self.build(inputs.shape)
self.built = True
return self.call(inputs)With automatic shape inference, our previous example becomes simple and neat:
model = models.Sequential([
SimpleDense(32, activation="relu"),
SimpleDense(64, activation="relu"),
SimpleDense(32, activation="relu"),
SimpleDense(10, activation="softmax"),
])Note that automatic shape inference is not the only thing that the Layer class’s __call__() method handles. It takes care of many more things, in particular routing between eager and graph execution (a concept you will learn about in chapter 7), and input making (which we will cover in chapter 11). For now, just remember: when implementing your own layers, put the forward pass in the call() method and the weight creation in the build() method.
From layers to models
A deep learning model is a graph of layers. In Keras, that’s the Model class. In Keras, that’s the Model class. Until now, you’ve only seen Sequential models (a subclass of Model), which are simple stacks of layers, mapping a single input to a single output. But as you move forward, you will be exposed to a much broader variety of network topologies. These are some common ones:
- Two-branch networks
- Multihead networks
- Residual connections
Network topology can get quite involved. For instance, figure 3.9 shows the topology of the graph of layers of a Transformer, a common architecture designed to process text data.
There are generally two ways of building such models in Keras: you could directly subclass the Model class, or you could use the Functional API, which lets you do more with less code. We will cover both the approaches in chapter 7.
The topology of a model defines a hypothesis space. You may remember that in chapter 1 we described machine learning as searching for useful representations of some input data, within a predefined space of possibilites, using guidance from a feedback signal. By choosing network topology, you constrain your space of possibilities (hypothesis space) to a specific series of tensor operations, mapping input data to output data. What you’ll then be searching for is a good set of value for the weight tensors involved in these tensor operations.
To learn from data, you have to make assumptions about it. These assumptions define what can be learned. As such, the structure of your hypothesis space - the architecture of your model - is extremely important. It encodes the assumptions you make about your problem, the prior knowledge that the model starts with. For instance, if you are working on a two-class classification problem with a model made of a single Dense layer with no activation (a pure affine transoformation), you are assuming that your two classes are linearly separable.
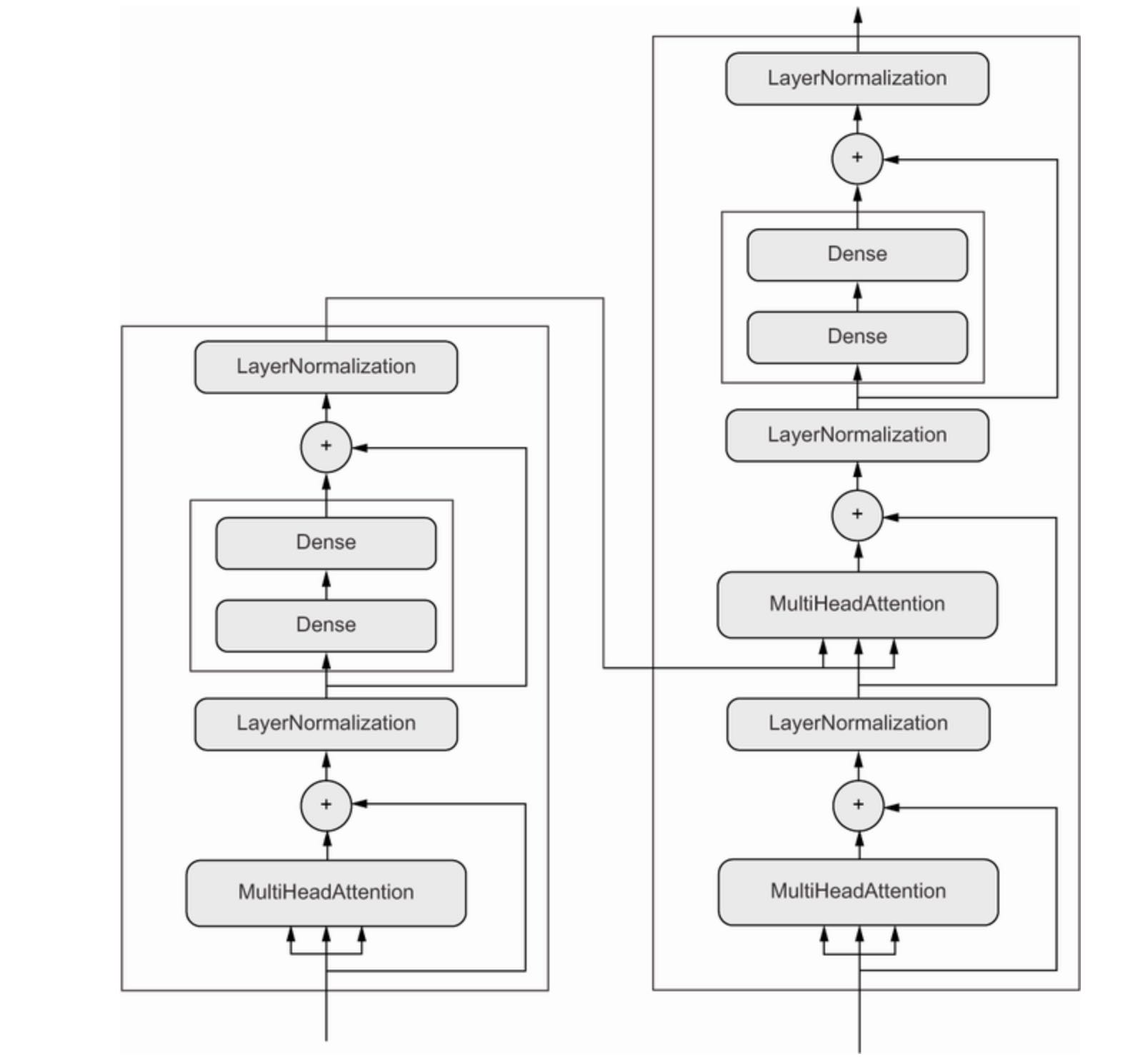
Picking the right network architecture is more an art than a science and although there are some best practices and principles you can rely on, only practice can help you become a proper neural-network architect. The next few chapters will both teach you explicitly principles for building neural networks and help you develop an intuition as to what works and what doesn’t. You’ll build a solid intuition about what type of model architectures work for different kinds of problems, how to build these netowks in practice, how to pick the right learning configuration, and how to tweak a model until it yields the results you want to see.
3.6.3 The “compile” step: Configuring the learning process
Once the model architecture is defined, you still have to choose three more things:
- Loss function (objective function): The quantity that will be minimized during training. It represents a measure of success for the task at hand.
- Optimizer: Determines how the network will be updated based on the loss function. It implements a specific variant of stochastic gradient descent (SGD).
- Metrics: The measures of success you want to monitor during training and validation, such as classification accuracy. Unlike the loss, training will not optimize directly for these metrics. As such, metrics don’t need to be differentiable.
Once you’ve picked your loss, optimizer, and metrics, you can use the built-in compile() and fit() methods to start training your model. Alternatively, you could also write your own custom training loops - we will cover how to do this in chapter 7. It’s a lot more work! For now, let’s take a look at compile() and fit().
The compile() method configures the training process - you’ve already been introduced to it in your very first neural network example in chapter 2. It takes the arguments optimizer, loss, and metrics (a list):
model = keras.Sequential([keras.layers.Dense(1)]) ## Define a linear classifier
model.compile(
optimizer="rmsprop", ## Specifies the optimizer by name: RMSprop (it's case sensitive)
loss="mean_squared_error", ## Specifies the loss by name: mean squared error
metrics=["accuracy"] ## Specify a list of metrics: in this case, only accuracy.
)In the preceding call to compile(), we passed the optimizer, loss, and metrics as strings(such as “rmsprop”). These strings are actually shortcuts that get converted to Python objects. For instance, “rmsprop” becomes keras.optimizers.RMSprop(). Importantly, it’s also possible to specify these arguments as object instances, like this:
model.compile(
optimizer=keras.optimizers.RMSprop(), ## Pass an optimizer instance: RMSprop
loss=keras.losses.MeanSquaredError(), ## Pass a loss instance: mean squared error
metrics=[keras.metrics.Accuracy()] ## Pass a list of metrics instances: in this case, only accuracy.
)This is useful if you want to pass your own custom losses or metrics, or if you want to further configure the objects you are using - for instance, by passing a learning_rate argument to the optimizer.
model.compile(
optimizer=keras.optimizers.RMSprop(learning_rate=1e-4), loss=my_custom_loss,
metrics=[my_custom_metric1, my_custom_metric2]
)In chapter 7, we will cover how to create custom losses and metrics. In general, you would not have to create your own losses, metrics or optimizers from scratch, because Keras offers a wide range of built-in options that is likely to include what you need:
Optimizers:
SGD( with or without momentum)RMSpropAdamAdagrad- Etc.
Losses:
CatagoricalCrossentropySparseCategoricalCrossentropyBinaryCrossentropyMeanSquaredErrorKLDivergenceCosineSimilarity- Etc.
Metrics:
CategoricalAccuracySparseCategoricalAccuracyBinaryAccuracyAUCPrecisionRecall- Etc.
Throughout this book, you will see concrete applications of many of these options.
3.6.4 Picking a loss function
Choosing the right loss function for the right problem is extremely important: your network will take any shortcut to minimize the loss, so if the objective doesn’t fully correlate with success for the task at hand, your network will end up doing something you may not have wanted. Imagine a stupid, omnipotent AI trained via SGD with the poorly chosen object function: “maximizing the average well-being of all humans alive”. To make its job easier, this AI might choose to kill all humans except a few and focus on the well-being of the remaining ones - because average well-being isn’t affected by how many humans are left. That might not be what you intended. Just remember that all neural networks you build will be just as ruthless in lowering their loss function - so choose the objective wisely, or you’ll have to face uninteded side effects.
Fortunately, when it comes to common problems such as classification, regression, and sequence prediction, there are simple guidelines you can follow to choose the correct loss. For instance, you will use binary crossentropy for a two-class classification problem, categorical crossentropy for a many-class classification problem, and so on. Only when you are working on a truly new research problems will you have to develop your own loss functions. In the next few chapters, we will detail explicitly which loss functions to choose for a wide range of common tasks.
3.6.5 Understanding the fit() method
After compile() comes fit(). The fit() method implements the training loop itself. These are its key arguments:
- The data (inputs and targets) to train on. It will typically be passed either in the form of NumPy arrays or a TensorFlow
Datasetobject. You will learn about theDatasetobject in the next chapters. - The number of epochs to train for: how many times the training loop should iterate over the data passed.
- The batch size to use within each epoch of mini-batch gradient descent: the number of training examples considered to compute the gradients for one weight update step.
## Listing 3.23 Calling fit() with NumPy data
history = model.fit(
inputs, ## The input examples, as NumPy array
targets, ## The corresponding training targets, as NumPy array
epochs=5, ## The training loop will iterate over the data 5 times
batch_size=128, ## The training loop will iterate over the data in batches of 128 examples.
)
The call to fit() returns a History object. This object contains a history field, which is a dict mapping keys such as “loss” or specific metric names to the list of their epoch values.
>>> history.history
{
"binary_accuracy": [0.5, 0.5, 0.5, 0.5, 0.5],
"loss": [0.6932, 0.6932, 0.6932, 0.6932, 0.6932] }
3.6.6 Monitoring loss and metrics on validation data
The goal of machine learning is not to obtain models that perform well on the training data which is easy - all you have to do is follow the gradient. The goal is to obtain models that perform well in general, and particularly on data points that the model has never encountered before. Just because a model performs well on its training data doesn’t mean it will perform well on data it has never seen! For instance, it’s possible that your model could end up merely memorizing a mapping between your training samples and their targets, which would be useless for the task of predicting targets for data the model has never seen before. We will go over this point in much more detail in chapter 5.
To keep an eye on how the model does on new data, it’s a standard practice to reserve a subset of the training data as validation data: you woun’t be training the model on this data, but you will use it to compute a loss value and metrics value. You do this by using the validation_data argument in the fit() method. Like the training data, the validation data could be passed as NumPy arrays or as TensorFlow Dataset objects.
## Listing 3.24 Using the validation_data argument
model = keras.Sequential([keras.layers.Dense(1)])
model.compile(
optimizer=keras.optimizers.RMSprop(learning_rate=0.1),
loss=keras.losses.MeanSquaredError(),
metrics=[keras.metrics.BinaryAccuracy()])
indices_permutation = np.random.permutation(len(inputs))
shuffled_inputs = inputs[indices_permutation] ## To avoid having samples from only one class in the validation data, shuffle the inputs and targets using a random indices permutation.
shuffled_targets = targets[indices_permutation]
num_validation_samples = int(0.3 * len(inputs)) ## Reserve 30% of the training inputs and targets for validation (we will exclude these samples from training and reserve them to compute the validation loss and metrics).
val_inputs = shuffled_inputs[:num_validation_samples]
val_targets = shuffled_targets[:num_validation_samples]
training_inputs = shuffled_inputs[num_validation_samples:]
training_targets = shuffled_targets[num_validation_samples:]
model.fit(
training_inputs, ## Training data, used to update the weights of the model.
training_targets,
epochs=5,
batch_size=16,
validation_data=(val_inputs, val_targets) ## Validation data, used only to monitor the validation loss and metrics.
)The value of the loss on the validation data is called the “validation loss”, to distinguish it from the “training loss”. Note that it’s essential to keep the training data and validation data strictly separate: the purpose of the validation is to monitor whether what the model is learning is actually useful on new data. If any of the validation data has been seen by the model during training, your validation loss and metrics will be flawed.
Note that if you want to compute the validation loss and metrics after the training is complete, you can call the evaluate() method:
loss_and_metrics = model.evaluate(val_inputs, val_targets, batch_size=128)evaluate() will iterate in batches (of size batch_size) over the data passed and return a list of scalars, where the first entry is the validation loss and the following entries are the validation metrics. If the model has no metrics, only the validation loss will be returned(rather than a list).
3.6.7 Inference: Using a model after training
Once you’ve trained your model, you are going to want to use it to make predictions on new data. This is called inference. To do this, a naive approach would simply be to __call__() the model:
predictions = model(new_inputs) ## Takes a NumPy array or TensorFlow tensor and returns a TensorFlow tensor.However, this will process all inputs in new_inputs at once, which may not be feasible if you’re looking at a lot of data ( in particular, it may require more memory than your GPU has).
A better way to do inference is to use the predict() method. It will iterate over the data in small batches and return a NumPy array of predictions. And unlike __call__(), it can also process TensorFlow Dataset objects.
predictions = model.predict(new_inputs, batch_size=128) ## Takes a NumPy array or TensorFlow Dataset and returns a NumPy array.For instance, if we use predict() on some of our validation data with linear model we trained earlier, we get scalar scores that correspond to the model’ prediction for each input sample:
>>> predictions = model.predict(val_inputs, batch_size=128)
>>> print(predictions[:10])
[[0.3590725]
[0.832981 ]
[0.1234567]
[0.5324567]
[0.9876543]
[0.2345678]
[0.3456789]
[0.456789 ]
[0.5678901]
[0.678901 ]]For now, this is all you need to know about Keras models. You are ready to move on to solving real-world machine learning problems with Keras in the next chapter.
Summary
- TensorFlow is an industry-strength numerical computing framework that can run on CPU, GPU or TPU. It can automatically compute the gradient of any differentiable expression, it can be distributed to many devices, and it can export programs to various external runtimes - even JavaScript.
- Keras is the standard API for doing deep learning with TensorFlow. It’s what we will use throughout the book.
- Key TensorFlow objects include tensors, variables, tensor operations and the gradient tape.
- The central class of Keras is the
Layer. A layer encapsulates some weights and some computation. Layers are assembled into models. - Before you start training a model, you need to pick an optimizer, a loss function, and some metrics, which you specify via the
model.compile()method. - To train a model, you can use the
model.fit()method, which runs mini-batch gradient descent for you. You can also use it to monitor your loss and metricss on validation data, a set of inputs that the model doesn’t see during training. - Once your model is trained, you use the
model.predict()method to generate predictions on new inputs.
