Deep Learning Chapter 4 Summary

Table of contents

• 4. Getting started with neural networks: Classification and regression

  • Classification and regression glossary

  • 4.1 Classifying movie reviews: a binary classification example

    • 4.1.1 THE IMDB dataset
    • 4.1.2 Preparing the data
    • 4.1.3 Building your network
    • 4.1.4 Validating your approach
    • 4.1.5 Using a trained network to generate predictions on new data
    • 4.1.6 Further experiments
    • 4.1.7 Wrapping up

  • 4.2 Classifying newswires: a multiclass classification example

    • 4.2.1 The Reuters dataset
    • 4.2.2 Preparing the data
    • 4.2.3 Building your model
    • 4.2.4 Validating your approach
    • 4.2.5 Generating predictions on new data
    • 4.2.6 A different way to handle the labels and the loss
    • 4.2.7 The importance of having sufficiently large intermediate layers
    • 4.2.8 Further experiments
    • 4.2.9 Wrapping up

  • 4.3 Predicting house prices: a regression example

    • 4.3.1 The Boston Housing Price dataset
    • 4.3.2 Preparing the data
    • 4.3.3 Building your model
    • 4.3.4 Validating your approach using K-fold validation
    • 4.3.5 Generating predictions on new data
    • 4.3.6 Wrapping up

  • Summary

• Gist

4. Getting started with neural networks: Classification and regression

This chapter is designed to get you started using neural networks to solve real problems. You will consolidate the knowledge you gained from chapters 2 and 3 and you will apply what you have learned to three new tasks covering the three most common use cases of neural networks - binary classification, multiclass classification, and scalar regression:

• Classifying movie reviews as positive or negative (binary classification)
• Classifying news wires by topic (multiclass classification)
• Estimating the price of a house, given real-estate data (regression)

These examples will be your first contact with end-to-end machine learning workflows: you will get introduced to data preprocessing, basic model architecture principles and model evaluation.

Classification and regression glossary

Classification and regression involve many specialized terms. You’ve come across some of them in earlier examples, and you will see more of them in future chapters. They have precise, machine learning specific definitions, and you should be familiar with them:

• Sample/input: One data point that goes into your model.
• Prediction/output: What comes out of your model.
• Target: The truth. What your model should ideally have predicted, according to an external source of data.
• Prediction error/loss value: A measure of the distance between your model’s prediction and the target.
• Classes: A set of possible labels to choose from in a classification problem. For example, when classifying cat and dog pictures, “dog” and “cat” are the two classes.
• Label: A specific instance of a class annotation in a classification problem. For instance, if picture #1234 is annotated as containing the class “dog”, then “dog” is a label of picture #1234.
• Ground-truth/annotations: All targets for a dataset, typically collected by humans.
• Binary classification: A classification task where each input sample should be categorized into two exclusive categories.
• Multiclass classification: A classification task where each input sample should be categorized into more than two categories: for instance, classifying handwritten digits.
• Multilabel classification: A classification task where each input sample can be assigned multiple labels. For instance, a given image may contain both a cat and a dog and should be annotated both with the “cat” label and the “dog” label. The number of labels per image is usually variable.
• Scalar regression: A task where the target is a continuous scalar value. Predicting house prices is a good example: the different target prices form a continuous space.
• Vector regression: A task where the target is a set of continuous values: for example, a continuous vector. If you are doing regression against multiple values (such as the coordinates of a bounding box in an image), then you are doing vector regression.
• Mini-batch/batch: A small set of samples (typically between 8 and 128) that are processed simultaneously by the model. The number of samples is often a power of 2, to facilitate memory allocation on GPU. When training, a mini-batch is used to compute a single gradient-descent update applied to the weights of the model.

By the end of this chapter, you will be able to use neural networks to handle simple classification and regression tasks over vector data. You will then be ready to start building more principled, theory-driven understanding of machine learning in chapter 5.

4.1 Classifying movie reviews: a binary classification example

Two-class classification, or binary classification, is one of the most common kinds of machine learning problems. In this example, you will learn to classify movie reviews as positive or negative, based on the text content of the reviews.

4.1.1 THE IMDB dataset

You will work with the IMDB dataset: a set of 50,000 highly polarized reviews from the Internet Movie Database. They are split into 25000 reviews for training and 25000 reviews for testing, each set consisting of 50% negative and 50% positive reviews.

Just like the MNIST dataset, the IMDB dataset comes packaged with Keras. It has already been preprocessed: the reviews (sequences of words) have been turned into sequences of integers, where each integer stands for a specific word in a dictionary. This enables us to focus on model building, training, and evaluation. In chapter 11, you will learn how to process raw text from scratch.

The following code will load the dataset (when you run it the first time, about 80MB of data will be downloaded to your machine):

from tensorflow.keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)

The argument num_words = 10000 means you will only keep the top 10,000 most frequently occurring words in the training data. Rare words will be discarded. This allows us to work with vector data of manageable size. If we didn’t set this limit, we’d be working with 88,585 unique words in the training data, which is unnecessarily large. Many of these words only occur in a single sample, and thus can’t be meaningfully used for classification.

The variables train_data and test_data are lists of reviews; each review is a list of word indices (encoding a sequence of words). train_labels and test_labels are lists of 0s and 1s, where 0 stands for negative and 1 stands for positive:

>>> train_data[0]
[1, 14, 22, 16, 43, 530, 973, 1622, 1385, 65, 458, 4468, 66, 3941, 4, 173, 36, 256, 5, 25, 100, 43, 838, 112, 50, 670, 2, 9, 35, 480, 284, 5, 150, 4, 172, 112, 167, 2, 336, 385, 39, 4, 172, 4536, 1111, 17, 546, 38, 13, 447, 4, 192, 50, 16, 6, 147, 2025, 19, 14, 22, 4, 1920, 4613, 469, 4, 22, 71, 87, 12, 16, 43, 530, 38, 76, 15, 13, 1247, 4, 22, 17, 515, 17, 12, 16, 626, 18, 2, 5, 62, 386, 12, 8, 316, 8, 106, 5, 4, 2223, 5244, 16, 480, 66, 3785, 33, 4, 130, 12, 16, 38, 619, 5, 25, 124, 51, 36, 135, 48, 25, 1415, 33, 6, 22, 12, 215, 28, 77, 52, 5, 14, 407, 16, 82, 2, 8, 4, 107, 117, 5952, 15, 256, 4, 2, 7, 3766, 5, 723, 36, 71, 43, 530, 476, 26, 400, 317, 46, 7, 4, 2, 1029, 13, 104]

>>> train_labels[0]
1

Because we are restricting ourselves to the top 10,000 most frequent words, no word index will exceed 10,000:

>>> max([max(sequence) for sequence in train_data])
9999

For kicks, here’s how you can quickly decode one of these reviews back to English words:

# Listing 4.2 Decoding reviews back to text

word_index = imdb.get_word_index()  ## word_index is a dictionary mapping words to an integer index.
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])  ## Reverses it, mapping integer indices to words.
decoded_review = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])  ## Decodes the review. Note that the indices are offset by 3 because 0, 1, and 2 are reserved indices for "padding", "start of sequence", and "unknown".

4.1.2 Preparing the data

You can’t directly feed lists of integers into a neural network. They all have different lengths, but a neural network expects to process contiguous batchs of data. You have to turn your lists into tensors. There are two ways to do that:

1. Pad your lists so that they all have the same length, turn them into an integer tensor of shape (samples, max_length), and start your model with a layer capable of handling such integer tensors (the Embedding layer, which we will cover in detail later).
2. Mutli-hot encode your lists to turn them into vectors of 0s and 1s. This would mean, for instance, turning the sequence [8, 5] into a 10,000-dimensional vector that would be all 0s except for indices 8 and 5, which would be 1s. Then you could use a Dense layer, capable of handling floating-point vector data, as the first layer in your model.

Let’s go with the latter solution. Here’s the code to vectorize the data, which you will do manually for maximum clarity:

# Listing 4.3 Encoding the integer sequences into via multi-hot encoding

import numpy as np
def vectorize_sequences(sequences, dimension=10000):
    results = np.zeros((len(sequences), dimension))  ## Creates an all-zero matrix of shape (len(sequences), dimension)
    for i, sequence in enumerate(sequences):
        for j in sequence:
            results[i, j] = 1.  ## Sets specific indices of results[i] to 1s
    return results
x_train = vectorize_sequences(train_data)  ## Vectorized training data
x_test = vectorize_sequences(test_data)  ## Vectorized test data

Here’s what the samples look like now:

>>> x_train[0]
array([0., 1., 1., ..., 0., 0., 0.])

You should also vectorize your labels, which is straightforward:

y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

Now the data is ready to be fed into a neural network.

4.1.3 Building your network

The input data is vectors, and the labels are scalars (1s and 0s): this is one of the simplest problem setup you will ever encounter. A type of model that performs well on such a problem is a plain stack of densely connected (Dense) layers with relu activations.

There are two key architecture decisions to be made about such a stack of Dense layers:

1. How many layers to use
2. How many units to choose for each layer

In chapter 5, you will learn formal principles to guide you in making these choices. For the time being, you will have to trust me with the following architecture choice:

1. Two intermediate layers with 16 units each
2. A third layer that will output the scalar prediction regarding the sentiment of the current review.

The next figure shows what the model looks like. And the following listing shows the Keras implementation, similar to the MNIST example you saw previously.

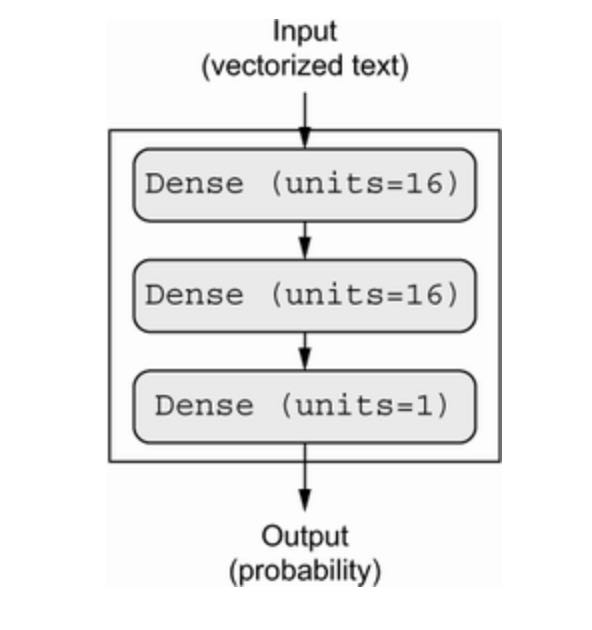
# Listing 4.4 Model definition

from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
    layers.Dense(16, activation='relu'),
    layers.Dense(16, activation='relu'),
    layers.Dense(1, activation='sigmoid')
])

The first argument being passed to each Dense layer is the number of units in the layer: the dimensionality of representation space of the layer. You remember from chapter 2 and 3 that each such Dense layer with a relu activation implements the following chain of tensor operations:

output = relu(dot(input, W) + b)

Having 16 units means the weight matrix W will have shape (input_dimension, 16), i.e. the dot product with W will project the input data onto a 16-dimensional representation space (and then you add the bias vector b and apply the relu operation). You can intuitively understand the dimensionality of your representation space as “how much freedom you are allowing the network to have when learning internal representations”. Having more units (a higher-dimensional representation space) allows your model to learn more complex representations, but it makes your model more computationally expensive and may lead to learning unwanted patterns (patterns that will improve performance on the training data but not on the test data).

The intermedia layers use relu as their activation function, and the final layer uses a sigmoid activation so as to output a probability (a score between 0 and 1, indicating how likely the sample is to have the target “1”: how likely the review is to be positive). A relu (rectified linear unit) is a function meant to zero out negative values, while a sigmoid “squashes” arbitrary values into the [0, 1] interval, outputting something that can be interpreted as a probability.

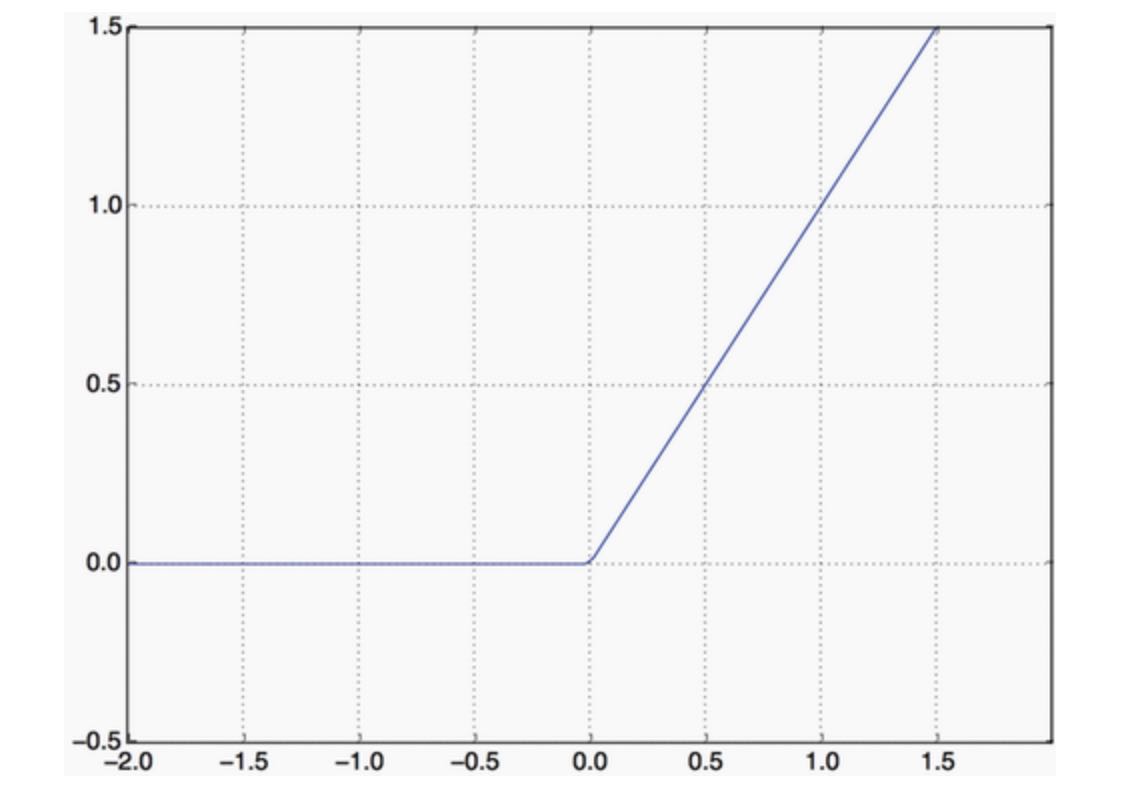
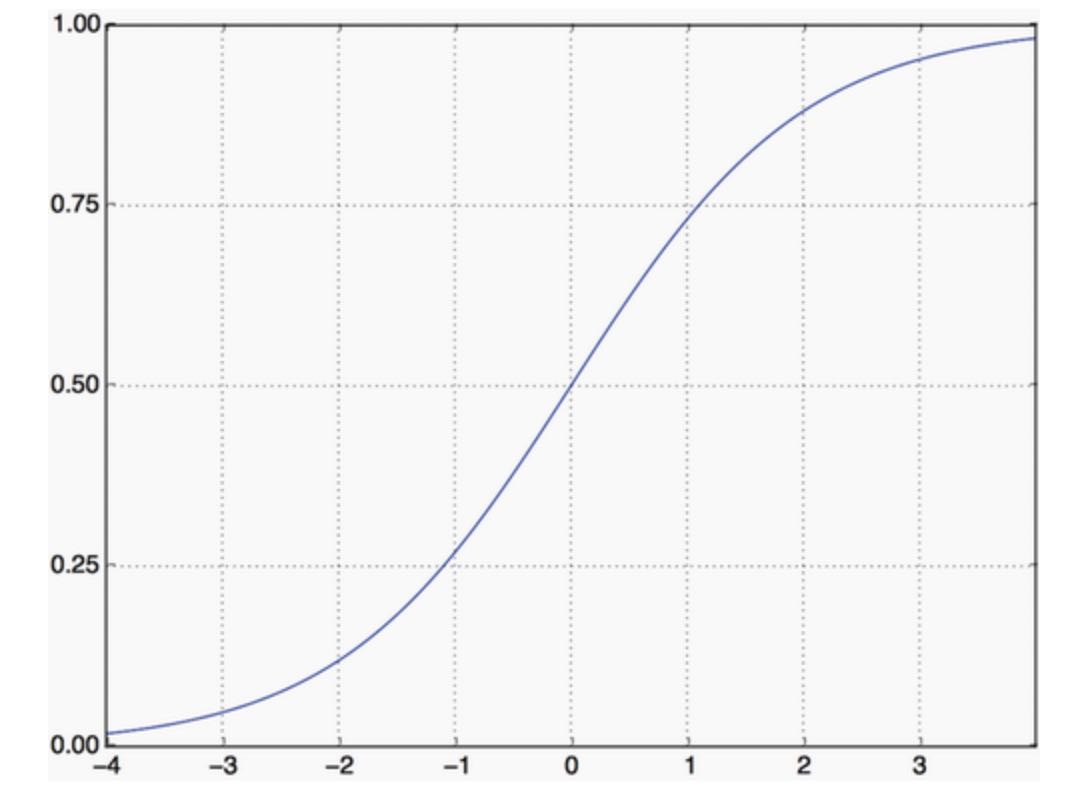
As for the choice of the optimizer, we will go with rmsprop, which is generally a good enough choice for virtually any problem.

WHAT ARE ACTIVATION FUNCTIONS AND WHY ARE THEY NECESSARY?

Without an activation function like relu(also called non-linearity), the Dense layer would consist of two linear operations (a dot product and an addition):

output = dot(W, input) + b

The layer could only learn linear transformations (affine transformations) of the input data: the hypothesis space of the layer would be the set of all possible linear transformations of the input data into a 16-dimensional space. Such a hypothesis space is too restricted and wouldn’t benefit from multiple layers of representations, because a deep stack of linear layers would still implement a linear operation: adding more layers wouldn’t extend the hypothesis space(as you saw in chapter 2).

In order to access to a much richer hypothesis space that would benefit from deep representations, you need a non-linearity, or activation function. relu is the most popular activation function in deep learning, but there are many other candidates, which all come with similarly strange names: prelu, elu, tanh, sigmoid, leaky_relu, etc.

Finally, you need to choose a loss function and an optimizer. Because you are facing a binary classification problem and the output of your model is a probability (you end your model with a single-unit layer with a sigmoid activation), it’s best to use the binary_crossentropy loss. It isn’t the only viable choice: you could use, for instance, mean_squared_error. But crossentropy is usually the best choice when you are dealing with models that output probabilities. Crossentropy is a quantity from the field of Information Theory that measures the distance between probability distributions or, in this case, between the ground-truth distribution and your predictions.

Here’s the step where we configure the model with the rmsprop optimizer and the binary_crossentropy loss function. Note that we will also monitor accuracy during training.

# Listing 4.5 Compiling the model

model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['accuracy'])

4.1.4 Validating your approach

As you learned in chapter 3, a deep learning should never be evaluated on its training data - its standard practice to use a validation set to monitor the accuracy of the model during training. Here, we will create a validation set by setting apart 10,000 samples from the original training data:

# Listing 4.6 Setting aside a validation set

x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]

We will now train the model for 20 epochs (20 iterations over all samples in the training data) in mini-batches of 512 samples. At the same time, we will monitor loss and accuracy on the 10,000 samples that we set apart. We do so by passing the validation data as the validation_data argument:

# Listing 4.7 Training your model

history = model.fit(partial_x_train,
                    partial_y_train,
                    epochs=20,
                    batch_size=512,
                    validation_data=(x_val, y_val))

On CPU, this will take less than 2 seconds per epoch - training is over in 20 seconds. At the end of every epoch, there is a slight pause as the model computes its loss and accuracy on the 10,000 samples of the validation data (as you have asked for “accuracy” metrics and provided validation_data).

Note that the call to model.fit() returns a History object, as you saw in chapter 3. This object has a member history, which is a dictionary containing data about everything that happened during training. Let’s take a look at it:

>>> history_dict = history.history
>>> history_dict.keys()
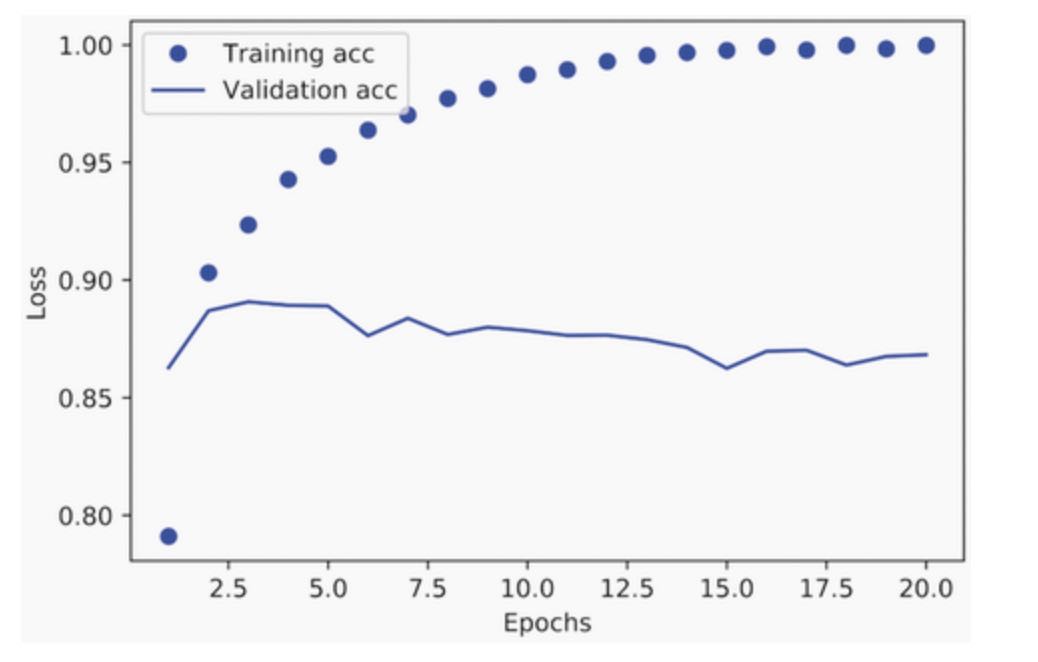
[u"accuracy", u"loss", u"val_accuracy", u"val_loss"]

The dictionary contains four entries: one per metric that was being monitored during training and during validation(there are 2 steps now, training and validation). In the following two listings, let’s use Matplotlib to plot the training and validation loss side by side(see figure 4.4), as well as the training and validation accuracy(see figure 4.5). Note that your own results may vary slightly due to a different random initialization of your model.

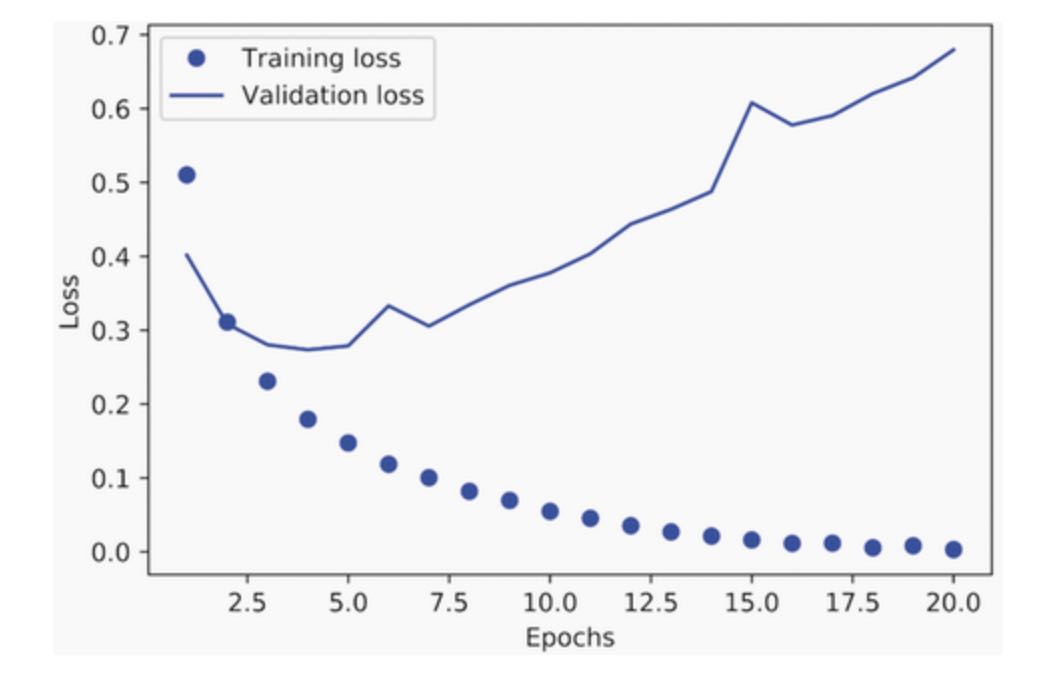
# Listing 4.8 Plotting the training and validation loss

import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')  ## "bo" is for "blue dot"
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')  ## "b" is for "solid blue line"
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

# Listing 4.9 Plotting the training and validation accuracy

plt.clf()  ## Clears the figure
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

As you can see, the training loss decreases with every epoch, and the training accuracy increases with every epoch. That’s what you would expect when running gradient-descent optimization - the quantity you are trying to minimize should be less with every iteration. But that isn’t the case for the validation loss and accuracy: they seem to peak at the fourth epoch. This is an example of what we warned against in chapter 3: a model that performs better on the training data isn’t necessarily a model that will do better on data it has never seen before. In precise terms, what you are seeing is overfitting: after the fourth epoch, you are over-optimizing on the training data, and you end up learning representations that are specific to the training data and do not generalize to data outside of the training set.

In this case, to prevent overfitting, you could stop training after four epochs. In general, you can use a range of techniques to mitigate overfitting, which we will cover in chapter 5.

Let’s train a new network from scratch for four epochs and then evaluate it on the test data:

# Listing 4.10 Retraining a model from scratch

model = keras.Sequential([
    layers.Dense(16, activation='relu'),
    layers.Dense(16, activation='relu'),
    layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)

The final results are as follows:

>>> results
[0.291, 0.883]  ## The first number 0.291 is the test loss and the second number 0.883 is the test accuracy

This fairly naive approach achieves an accuracy of 88%. With state-of-the-art approaches, you should be able to get close to 95%.

4.1.5 Using a trained network to generate predictions on new data

After having trained a model, you will want to use it in a practical setting. You can generate the likelihood of reviews being positive by using the predict method, as you have learned in chapter 3:

>>> model.predict(x_test)
array([[ 0.98 ]
    [ 0.01 ]
    [ 0.91 ]
    ...
    [ 0.43 ]
    [ 0.99 ]
    [ 0.73 ]]
    ], dtype=float32)

As you can see the model is confident for some samples (0.99 or more, or 0.01 or less) but less confident for others (0.6, 0.4).

4.1.6 Further experiments

The following experiments will help convince you that the architecture choices you have made are all fairly reasonable, although there is still room for improvement:

• You used two representation layers before the final classification layer. Try using one or three representation layers, and see how doing so affects validation and test accuracy.
• Try using layers with more units or fewer units: 32 units, 64 units, and so on.
• Try using the mse loss function instead of binary_crossentropy.
• Try using the tanh activation (an activation that was popular in the early days of neural networks) instead of relu.

4.1.7 Wrapping up

Here’s what you should take away from this example:

• You usually need to do quite a bit of preprocessing on your raw data in order to be able to feed it - as tensors - into a neural network. Sequences of words can be encoded as binary vectors, but there are other encoding options, too.
• Stacks of Dense layers with relu activations can solve a wide range of problems (including sentiment classification), and you will likely use them frequently.
• In a binary classification problem (two output classes), your network should end with a Dense layer with one unit and a sigmoid activation: the output of your network should be a scalar between 0 and 1, encoding a probability.
• With such a scalar sigmoid output on a binary classification problem, the loss function you should use is binary_crossentropy.
• The rmsprop optimizer is generally a good enough choice of optimizer, whatever your problem. That’s one less thing for you to worry about.
• As they get better on their training data, neural networks eventually start overfitting and end up obtaining increasingly worse results on data they have never seen before. Make sure to always monitor performance on data that is outside of the training set.

4.2 Classifying newswires: a multiclass classification example

In the previous section, you saw how to classify vector inputs into two mutually exclusive classes using a densely connected neural network. But what happens when you have more than two classes?

In this section, we will build a model to classify Reuters newswires into 46 mutually exclusive topics. Because we have many classes, this problem is an instance of multiclass classification; and because each data point should be classified into only one category, the problem is more specifically an instance of single-label, multiclass classification. If each data point could belong to multiple categories (in this case, topics), you would be facing a multilabel, multiclass classification problem.

4.2.1 The Reuters dataset

You will work with the Reuters dataset, a set of short newswires and their topics, published by Reuters in 1986. It’s a simple, widely used toy dataset for text classification. There are 46 different topics; some topics are more represented than others, but each topic has at least 10 examples in the training set.

Like IMDB and MNIST, the Reuters dataset comes packaged with Keras. Let’s take a look at how you can load it:

# Listing 4.11 Loading the Reuters dataset

from tensorflow.keras.datasets import reuters
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)

As with the IMDB dataset, the argument num_words = 10000 restricts the data to the 10,000 most frequently occurring words found in the data.

You have 8,982 training examples and 2,246 test examples:

>>> len(train_data)
8982
>>> len(test_data)
2246

As with the IMDB reviews, each example is a list of integers (word indices):

>>> train_data[10]
[1, 245, 273, 207, 156, 53, 74, 160, 26, 14, 46, 296, 26, 39, 74, 2979, 3554, 14, 46, 4689, 4329, 86, 61, 3499, 4795, 14, 61, 451, 4329, 17, 12]

Here’s how you can decode it back to words:

# Listing 4.12 Decoding newswires back to text

word_index = reuters.get_word_index()
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
decoded_newswire = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])  ## Note that the indices are offset by 3 because 0, 1, and 2 are reserved indices for "padding", "start of sequence", and "unknown".

The label associated with an example is an integer between 0 and 45 - a topic index:

>>> train_labels[10]
3

4.2.2 Preparing the data

You can vectorize the data with the exact same code as in the previous example:

# Listing 4.13 Encoding the input data

x_train = vectorize_sequences(train_data)  ## Vectorized training data
x_test = vectorize_sequences(test_data)  ## Vectorized test data

To vectorize the labels, there are two possibilities: you can cast the label list as an integer tensor, or you can use one-hot encoding. One-hot encoding is a widely used format for categorical data, also called categorical encoding. In this case, one-hot encoding of the labels consists of embedding each label as an all-zero vector with a 1 in the place of the label index. Here’s how you can one-hot encode the labels:

# Listing 4.14 Encoding the labels

def to_one_hot(labels, dimension=46):
    results = np.zeros((len(labels), dimension))
    for i, label in enumerate(labels):
        results[i, label] = 1.
    return results

y_train = to_one_hot(train_labels)  ## Vectorized training labels
y_test = to_one_hot(test_labels)  ## Vectorized test labels

Note that there is a built-in way to do this in Keras:

from tensorflow.keras.utils import to_categorical
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)

4.2.3 Building your model

This topic classification problem looks similar to the previous movie review classification problem: in both cases, you are trying to classify short snippets of text. But there is a new constraint here: the number of output classes has gone from 2 to 46. The dimensionality of the output space is much larger.

In a stack of Dense layerss like those we have been using, each layer can only access information present in the output of the previous layer. If one layer drops some information relevant to the classification problem, this information can never be recovered by later layers: each layer can potentially become an information bottleneck. In the previous example, you used 16-dimensional intermediate layers, but a 16-dimensional space may be too limited to learn to separate 46 different classes: such small layers may act as information bottlenecks, permanently dropping relevant information.

For this reason, we will use larger layers. Let’s go with 64 units:

# Listing 4.15 Model definition
model = keras.Sequential([
    layers.Dense(64, activation='relu'),
    layers.Dense(64, activation='relu'),
    layers.Dense(46, activation='softmax')
])

There are two other things you should note about this architecture:

1. We end the model with a Dense layer of size 46. This means for each input sample, the network will output a 46-dimensional vector. Each entry in this vector (each dimension) will encode a different output class.
2. The last layer uses a softmax activation. You saw this pattern in the MNIST example. It means the network will output a probability distribution over the 46 different output classes - for every input sample, the network will produce a 46-dimensional output vector, where output[i] is the probability that the sample belongs to class i. The 46 scores will sum to 1.

The best loss function to use in this case is categorical_crossentropy. It measures the distance between two probability distributions: here, between the probability distribution output by the network and the true distribution of the labels. By minimizing the distance between these two distributions, you train the network to output something as close as possible to the true labels.

# Listing 4.16 Compiling the model

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

4.2.4 Validating your approach

Let’s set apart 1,000 samples in the training data to use as a validation set:

# Listing 4.17 Setting aside a validation set

x_val = x_train[:1000]
partial_x_train = x_train[1000:]
y_val = y_train[:1000]
partial_y_train = y_train[1000:]

Now let’s train the model for 20 epochs:

# Listing 4.18 Training the model

history = model.fit(partial_x_train,
                    partial_y_train,
                    epochs=20,
                    batch_size=512,
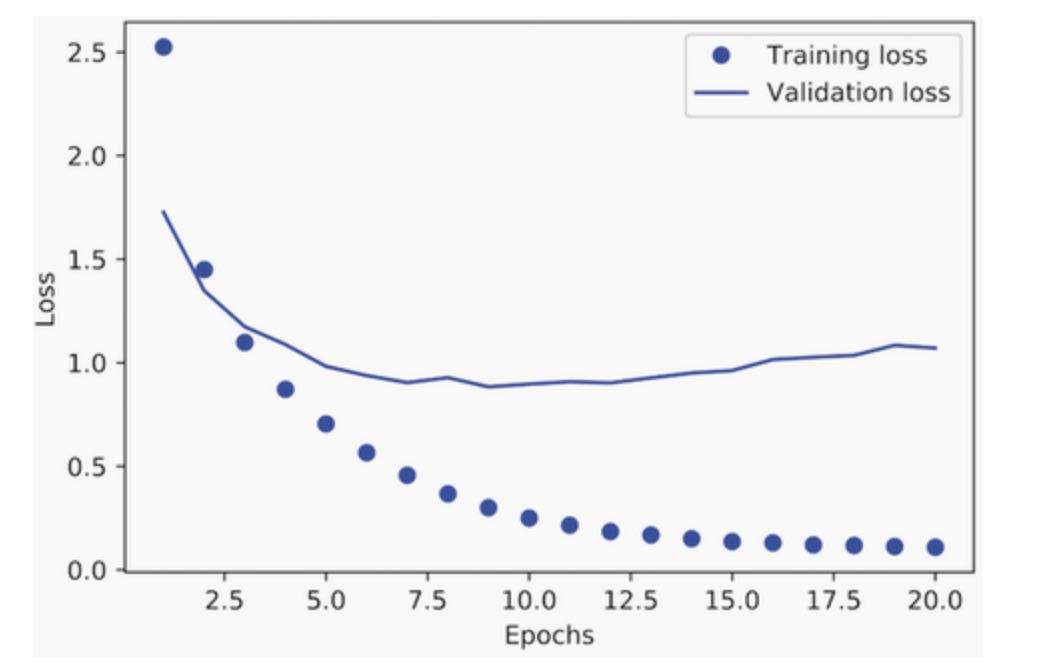
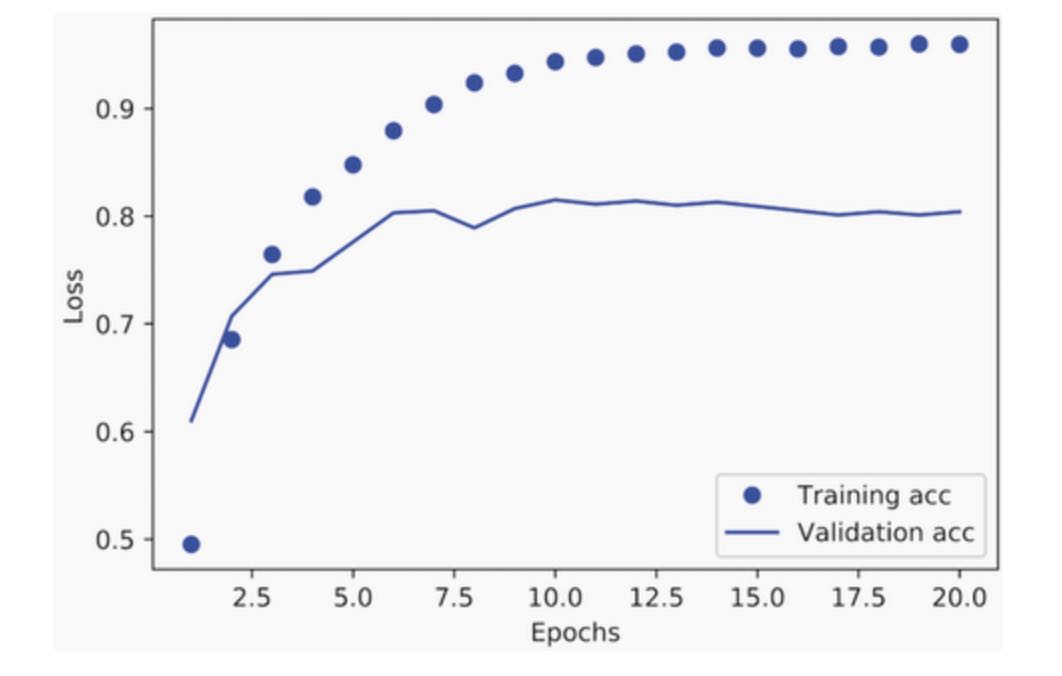
                    validation_data=(x_val, y_val))

Let’s display its loss and accuracy curves:

# Listing 4.19 Plotting the training and validation loss

import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

# Listing 4.20 Plotting the training and validation accuracy

plt.clf()
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

The model begins to overfit after nine epochs. Let’s train a new model from scratch for nine epochs and then evaluate it on the test set:

# Listing 4.21 Retraining a model from scratch

model = keras.Sequential([
    layers.Dense(64, activation='relu'),
    layers.Dense(64, activation='relu'),
    layers.Dense(46, activation='softmax')
])

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

model.fit(partial_x_train,
            partial_y_train,
            epochs=9,
            batch_size=512,
            validation_data=(x_val, y_val))

results = model.evaluate(x_test, one_hot_test_labels)

The final results are as follows:

>>> results
[0.959, 0.796]

This approach reaches an accuracy of ~80%. With a balanced binary classification problem, the accuracy reached by a purely random classifier would be 50%. But in this case, we have 46 classes, and they may not be equally represented. What would be the accuracy of a random baseline? We could try quickly implementing one to check this empirically:

>>> import copy
>>> test_labels_copy = copy.copy(test_labels)
>>> np.random.shuffle(test_labels_copy)
>>> hits_array = np.array(test_labels) == np.array(test_labels_copy)
>>> print(hits_array.mean())
0.18655387355298308

As you can see, a random classifier would have achieved an accuracy of ~19%, so the results of the previous approach are pretty good in that light.

4.2.5 Generating predictions on new data

Calling the model’s predict method on new samples returns a class probability distribution over all 46 topics. Let’s generate topic predictions for all of the test data:

>>> predictions = model.predict(x_test)

Each entry in predictions is a vector of length 46:

>>> predictions[0].shape
(46,)

The coefficients in this vector sum to 1, as they form a probability distribution:

>>> np.sum(predictions[0])
1.0

The largest entry is the predicted class - the class with the highest probability:

>>> np.argmax(predictions[0])
4

4.2.6 A different way to handle the labels and the loss

We mentioned earlier that another way to encode the labels would be to cast them as an integer tensor, like such:

y_train = np.array(train_labels)
y_test = np.array(test_labels)

The only thing this approach would change is the choice of the loss function. The loss function categorical_crossentropy expects the labels to follow a categorical encoding. With integer labels, you should use sparse_categorical_crossentropy:

model.compile(optimizer='rmsprop',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

This new loss function is still mathematically the same as categorical_crossentropy; it just has a different interface.

4.2.7 The importance of having sufficiently large intermediate layers

We mentioned earlier that because the final outputs are 46-dimensional, you should avoid intermediate layers with many fewer than 46 hidden units. Now let’s see what happens when you introduce an information bottleneck by having intermediate layers that are significantly less than 46-dimensional, e.g. 4-dimensional:

# Listing 4.22 A model with an information bottleneck

model = keras.Sequential([
    layers.Dense(64, activation='relu'),
    layers.Dense(4, activation='relu'),
    layers.Dense(46, activation='softmax')
])
model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])
model.fit(partial_x_train,
            partial_y_train,
            epochs=20,
            batch_size=128,
            validation_data=(x_val, y_val))

The model now peaks at ~71% validation accuracy, an 8% absolute drop. This drop is mostly due to the fact that you are trying to compress a lot of information (enough information to recover the separation hyperplanes of 46 classes) into an intermediate space that is too low-dimensional. The model is able to cram most of the necessary information into these four-dimensional representations, but not all of it.

4.2.8 Further experiments

Like in our previous example, I encourage you to try out the following experiments to take your intuition about the kind of configuration decisions you have to make with such models:

• Try using larger or smaller layers: 32 units, 128 units, and so on.
• You used two intermediate layers before the final softmax classification layer. Now try using a single intermediate layer, or three intermediate layers.

4.2.9 Wrapping up

Here’s what you should take away from this example:

• If you are trying to classify data points between N classes, your network should end with a Dense layer of size N.
• In a single-label, multiclass classification problem, your network should end with a softmax activation, so that it will output a probability distribution over the N output classes.
• Categorical crossentropy is almost always the loss function you should use for such problems. It minimizes the distance between the probability distributions output by the network and the true distribution of the targets.
• There are two ways to handle labels in multiclass classification:
  • Encoding the labels via categorical encoding (also known as one-hot encoding) and using categorical_crossentropy as your loss function.
  • Encoding the labels as integers and using sparse_categorical_crossentropy as your loss function.
• If you need to classify data into a large number of categories, you should avoid creating information bottlenecks in your network by having intermediate layers that are too small.

4.3 Predicting house prices: a regression example

The two previous examples were considered classification problems, where the goal was to predict a single discrete label of an input data point. Another common type of machine learning problem is regression, which consists of predicting a continuous value instead of a discrete label. For instance, predicting the temperature tomorrow, given meteorological data, or predicting the time that a software project will take to complete, given its specifications.

NOTE: Don’t confuse regression and logistic regression algorithm. Confusingly, logistic regression isn’t a regression algorithm - it’s a classification algorithm.

4.3.1 The Boston Housing Price dataset

In this section, we will attempt to predict the median price of homes in a given Boston suburb in the mid-1970s, given data points about the suburb at the time, such as the crime rate, the local property tax rate, etc. The dataset we will use has an interesting difference from the two previous examples. It has relatively few data points: only 506, split between 404 training samples and 102 test samples. And each “feature” in the input data (e.g. the crime rate) has a different scale. For instance, some values are proportions, which take values between 0 and 1; others take values between 1 and 12, others between 0 and 100, etc.

# Listing 4.23 Loading the Boston Housing Price dataset

from tensorflow.keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

Let’s take a look at the data:

>>> train_data.shape
(404, 13)
>>> test_data.shape
(102, 13)

As you can see, you have 404 training samples and 102 test samples, each with 13 numerical features, such as per capita crime rate, average number of rooms per dwelling, accessibility to highways, etc.

The targets are the median values of owner-occupied homes, in thousands of dollars:

>>> train_targets
[15.2, 42.3, 50. ... 19.4, 19.4, 29.1]

The prices are typically between $10,000 and $50,000. If that sounds cheap, remember that this data is from the mid-1970s and these prices aren’t adjusted for inflation.

4.3.2 Preparing the data

It would be problematic to feed into a neural network values that all take wildly different ranges. The model might be able to automatically adapt to such heterogeneous data, but it would definitely make learning more difficult. A widespread best practice for dealing with such data is to do a feature-wise normalization: for each feature in the input data (a column in the input data matrix), we subtract the mean of the feature and divide by the standard deviation, so that the feature is centered around 0 and has a unit standard deviation. This is easily done in Numpy:

# Listing 4.24 Normalizing the data

mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

test_data -= mean
test_data /= std

Note that the quantities used for normalizing the test data are computed using the training data. You should never use any quantity computed on the test data, in your workflow, even for something as simple as data normalization.

4.3.3 Building your model

Because so few samples are available, we will use a very small model with two intermediate layers, each with 64 units. In general, the less training data you have, the worse overfitting will be, and using a small model is one way to mitigate overfitting.

# Listing 4.25 Model definition

def buid_model():
    model = keras.Sequential([  ## Because we will need to instantiate the same model multiple times, we use a function to construct it.
        layers.Dense(64, activation='relu'),
        layers.Dense(64, activation='relu'),
        layers.Dense(1)
    ])
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model

The model ends with a single unit and no activation (it will be a linear layer). This is a typical setup for scalar regression (a regression where you are trying to predict a single continuous value). Applying an activation function would constrain the range that the output can take; for instance, if you applied a sigmoid activation function to the last layer, the model could only learn to predict values between 0 and 1. Here, because the last layer is purely linear, the model is free to learn to predict values in any range.

Note that we compile the model with the mse loss function - Mean Squared Error, the square of the difference between the predictions and the targets. This is a widely used loss function for regression problems.

We are also monitoring a new metric during training: Mean Absolute Error (MAE). It is the absolute value of the difference between the predictions and the targets. For instance, an MAE of 0.5 on this problem would mean your predictions are off by $500 on average.

4.3.4 Validating your approach using K-fold validation

To evaluate our model we keep adjusting the parameters (such as the number of epochs used for training), we could split the data into a training set and a validation set, as we did in the previous examples. But because we have so few data points, the validation set would end up being very small (e.g. about 100 examples). As a consequence, the validation scores might change a lot depending on which data points you chose to use for validation and which you chose for training: the validation scores might have a high variance with regard to the validation split. This would prevent you from reliably evaluating your model.

The best practice in such situations is to use K-fold cross-validation.

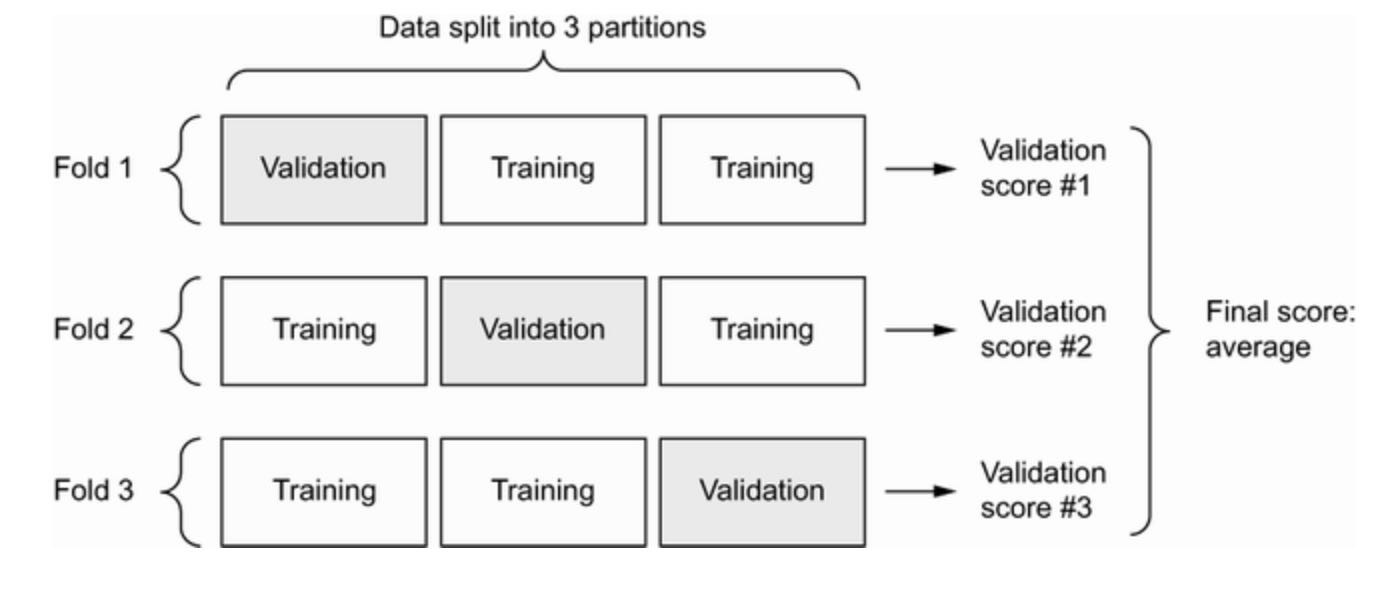
It consists of splitting the available data into K partitions (typically K = 4 or 5), instantiating K identical models, and training each one on K - 1 partitions while evaluating on the remaining partition. The validation score for the model used is then the average of the K validation scores obtained. In terms of code, this is straightforward:

# Listing 4.26 K-fold validation

k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []

for i in range(k):
    print(f'Processing fold #{i}')
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]  ## Prepares the validation data: data from partition #k
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
    partial_train_data = np.concatenate(  ## Prepares the training data: data from all other partitions
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)
    model = build_model()  ## Builds the Keras model (already compiled)
    model.fit(partial_train_data, partial_train_targets, epochs=num_epochs, batch_size=16, verbose=0)  ## Trains the model (in silent mode, verbose=0)
    val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)  ## Evaluates the model on the validation data
    all_scores.append(val_mae)

Running this with num_epochs = 100 yields the following results:

>>> all_scores
[2.112449, 3.0801501, 2.6483836, 2.4275346]
>>> np.mean(all_scores)
2.5671294

The different runs do indeed show rather different validation scores, from 2.1 to 3.1. The average (2.6) is a much more reliable metric than any single score - that’s the entire point of K-fold cross-validation. In this case, you are off by $2,600 on average, which is significant considering that the prices range from $10,000 to $50,000.

Let’s try training the model a bit longer: 500 epochs. To keep a record of how well the model does at each epoch, you will modify the training loop to save the per-epoch validation score log for each fold:

# Listing 4.27 Saving the validation logs at each fold

num_epochs = 500
all_mae_histories = []

for i in range(k):
    print(f'Processing fold #{i}')
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]  ## Prepares the validation data: data from partition #k
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
    partial_train_data = np.concatenate(  ## Prepares the training data: data from all other partitions
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)
    model = build_model()  ## Builds the Keras model (already compiled)
    history = model.fit(partial_train_data, partial_train_targets,  ## Trains the model (in silent mode, verbose=0)
                        validation_data=(val_data, val_targets), epochs=num_epochs, batch_size=16, verbose=0)
    mae_history = history.history['val_mae']
    all_mae_histories.append(mae_history)

We can then compute the average of the per-epoch MAE scores for all folds:

# Listing 4.28 Building the history of successive mean K-fold validation scores

average_mae_history = [
    np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)
]

Let’s plot this:

# Listing 4.29 Plotting validation scores

import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()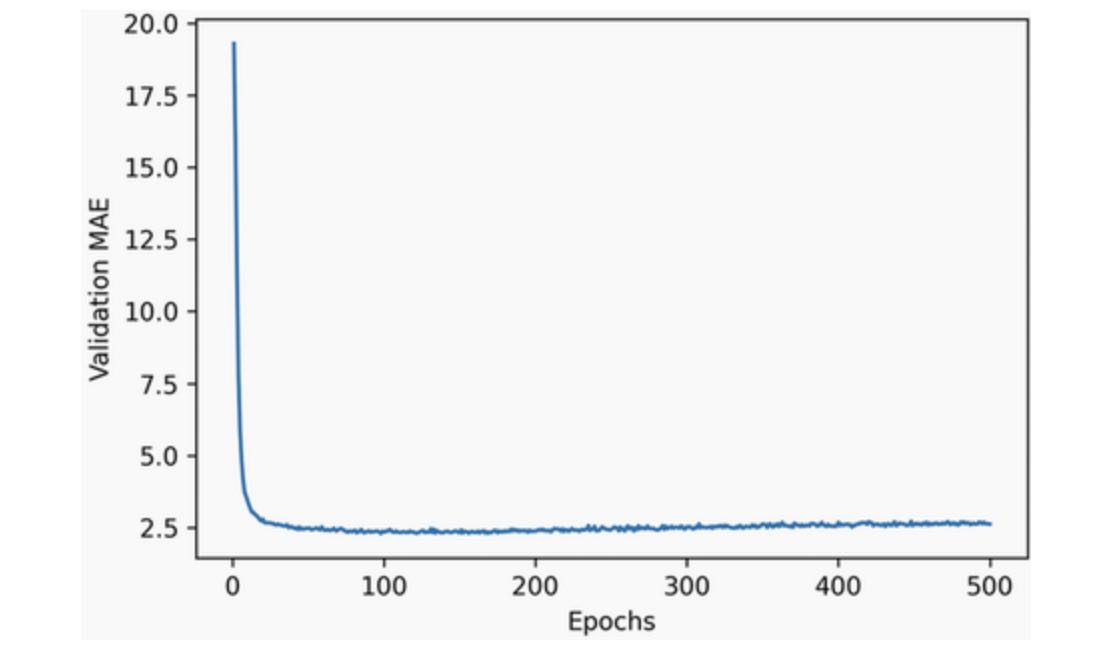

It may be a little difficult to read the plot due to scaling issue: the validation MAE for the first few epochs is significantly higher than the values that follow. Let’s omit the first 10 data points, which are on a different scale from the rest of the curve, for clearer visualization:

# Listing 4.30 Plotting validation scores, excluding the first 10 data points

truncated_mae_history = average_mae_history[10:]
plt.plot(range(1, len(truncated_mae_history) + 1), truncated_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()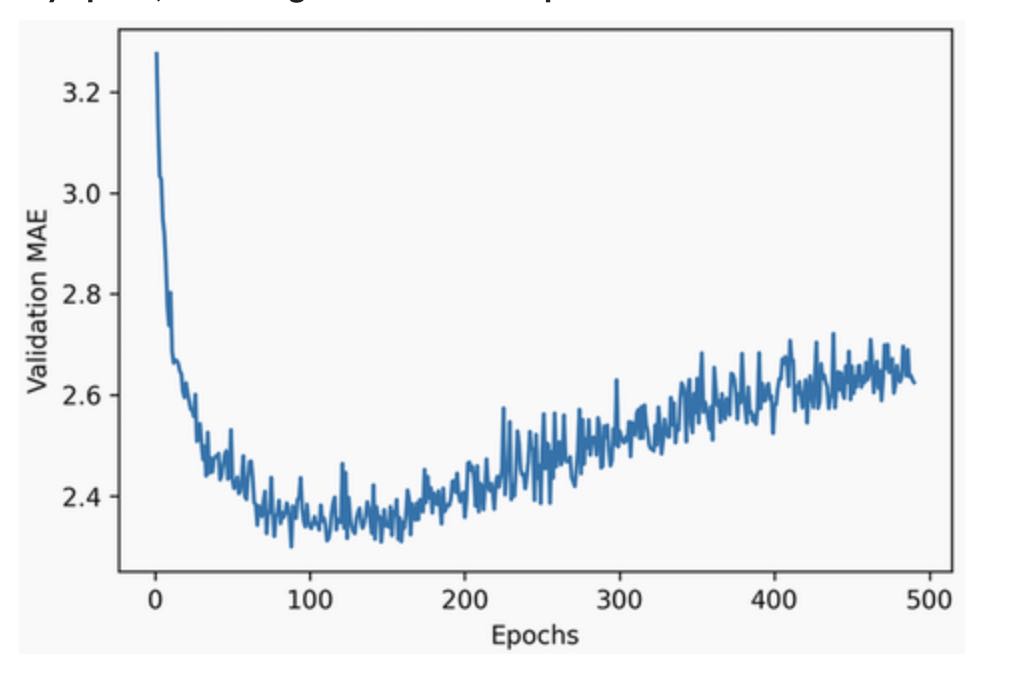

As you can see in the plot, validation MAE stops improving significantly after 120 epochs (this number includes the 10 epochs we omitted). Past that point, you start overfitting.

Once you are finished tuning other parameters of your model (in addition to the number of epochs, you could also adjust the size of the intermediate layers), you can train a final “production” model on all of the training data, with the best parameters, and then look at its performance on the test data:

# Listing 4.31 Training the final model

model = build_model()  ## Gets a fresh, compiled model
model.fit(train_data, train_targets,
            epochs=130, batch_size=16, verbose=0)  ## Trains it on the entirety of the data
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

Here’s the final result:

>>> test_mae_score
2.4642276763916016

We are still off by a bit under $2,500. It’s an improvement! Just like with the two previous tasks, you can try varying the number of layers in the model, or the number of units per layer, to see if you can squeeze out a lower test error.

4.3.5 Generating predictions on new data

When calling predict() on our binary classification model, we retrieved a scalar score between 0 and 1. With our multiclass classification model, we retrieved a probability distribution over all classes for each sample. Now, with this scalar regression model, predict() returns the model’s guess for the sample priice in thousands of dollars:

>>> model.predict(test_data)
>>> predictions[0]
array([9.990133], dtype=float32)

The first house in the test set is prediction to have a price of about $10,000.

4.3.6 Wrapping up

Here;s what you should take away from this scalar regression example:

• Regression is done using different loss functions than what we used for classification. Mean Squared Error (MSE) is a loss function commonly used for regression.
• Similarly, evaluation metrics to be used for regression differ from those used for classification; naturally, the concept of “accuracy” does not apply for regression. A common regression metric is Mean Absolute Error (MAE).
• When features in the input data have values in different ranges, each feature should be scaled independently as a preprocessing step.
• When there is little data available, using K-fold cross-validation is a great way to reliably evaluate a model.
• When little training data is available, it is preferable to use a small model with few intermediate layers (typically only one or two), in order to avoid severe overfitting.

Summary

• The three most common kinds of machine learning tasks on vector data are binary classification, multiclass classification, and scalar regression.
  • The “Wrapping Up” sections earlier in the chapter summarize the most important points you have learned regarding each task.
  • Regression uses different loss functions and evaluation metrics than classification.
• You will usually need to preprocess raw data before feeding it into a neural network.
• When your data has features with different ranges, scale each feature independently as part of preprocessing.
• As training progresses, neural networks eventually begine to overfit and obtain worse results on never-before-seen data.
• If you don’t have much training data, use a small model with only one or two intermediate layers to avoid severe overfitting.
• If your data is divided into many categories, you may cause an information bottleneck if you use intermediate layers that are too small.
• When you are working with little data, K-fold validation can help reliably evaluate your model.

Gist

Previous Chapter Next Chapter