Deep Learning Chapter 2 Summary

Table of contents

• 2. The mathematical building blocks of neural networks

  • 2.1 A first look at a neural network

  • 2.2 Data representations for neural networks

    • 2.2.1 Scalars (rank-0 tensors)
    • 2.2.2 Vectors (rank-1 tensors)
    • 2.2.3 Matrices (rank-2 tensors)
    • 2.2.4 Rank-3 and higher-rank tensors
    • 2.2.5 Key attributes
    • 2.2.6 Manipulating tensors in NumPy
    • 2.2.7 The notion of data batches
    • 2.2.8 Real-world examples of data tensors
    • 2.2.9 Vector data
    • 2.2.10 Timeseries data or sequence data
    • 2.2.11 Image data
    • 2.2.12 Video data

  • 2.3 The gears of neural networks: tensor operations

    • 2.3.1 Element-wise operations
    • 2.3.2 Broadcasting
    • 2.3.3 Tensor product
    • 2.3.4 Tensor reshaping
    • 2.3.5 Geometric interpretation of tensor operations
    • 2.3.6 A geometric interpretation of deep learning

  • 2.4 The engine of neural networks: gradient-based optimization

    • 2.4.1 What’s a derivative?
    • 2.4.2 Derivative of a tensor operation: the gradient
    • 2.4.3 Stochastic gradient descent
    • 2.4.4 Chaining Derivatives: The Backpropagation Algorithm

  • 2.5 Looking back at our first example

    • 2.5.1 Reimplementing our first example from scratch in TensorFlow
    • 2.5.2 Running one training step
    • 2.5.3 The full training loop
    • 2.5.4 Evaluating the model

  • SUMMARY:

2. The mathematical building blocks of neural networks

Understanding deep learning requires familiarity with many simple mathematical concepts: tensors, tensor operations, differentiation, gradient descent and so on. Our goal is to build up the intution about these notions without getting overly technical.

We will not use mathematical notations. The most precise, unambiguous description of a mathematical operation is its executable code.

To provide sufficient context for introducing tensors and gradient descent, we will begin the chapter with a practical example of a neural network. Then we will go over every new concept that’s been introduced, point by point. The concepts will be essential to understand the practical examples in the following chapters.

After reading this chapter, you will have an intuitive understanding of the mathematical theory behind deep learning, and you will be ready to start diving into Keras and TensorFlow in chapter 3.

2.1 A first look at a neural network

Let’s look at a concrete example of a neural network that uses the Python library to learn to classify handwritten digits. Don’t worry if some steps seem arbitrary or look like magic to you. We’ve got to start somewhere.

The problem we are trying to fix here is to classify grayscale images of handwritten digits (28x28 pixels) into their 10 categories (0 through 9). We will using MNIST dataset, a classic in the machine learning community. It’s a set of 60000 training images, plus 10000 test images, assembled by the National Institute of Standards and Technology (the NIST in MNIST) in the 1980s. You can think of “solving” MNIST as the “Hello World” of deep learning

Note: In ML, a category in a classification problem is called a class. Data points are called samples. The class of a specific sample is called a label.

The MNIST dataset comes preloaded in Keras, in the form of a set of four NumPy arrays:

from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images and train_labels form the “training set”, the data that the model will learn from.

The model will then be tested on the test set, test_images and test_labels

The images are encoded as NumPy arrays, and the labels are an array of digits, ranging from 0 to 9. The images and labels have a one-to-one correspondence.

Let’s look at training data:

>>> train_images.shape
(60000, 28, 28)
>>> len(train_labels)
60000
>>> train_labels
array([5, 0, 4, ..., 5, 6, 8], dtype=uint8)

and here’s the test data:

>>> test_images.shape
(10000, 28, 28)
>>> len(test_labels)
10000
>>> test_labels
array([7, 2, 1, ..., 4, 5, 6], dtype=uint8)

The workflow will be as follows: First, we will feed the neural network the training data, train_images and train_labels. The network will then learn to associate images and labels. Finally, we will ask the network to produce predictions for test_images, and we will verify whether these predictions match the labels from test_labels.

Let’s build the network:

from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
    layers.Dense(512, activation='relu'),
    layers.Dense(10, activation='softmax')
])

The core building block of neural networks is the layer. You can think of layer as a filter for data: some data goes in and out comes a more useful form. Specifically, laerys extract representations out of the data fed into them. Most of the deep learning consists of chaining together simple layers that will implement a form of progressive data distillation. A deep learning model is like a sieve for data processing, made of a succession of increasingly refined data filters - the layers.

Here, our model consists of a sequence of two Dense layers, which are densely connected (also called fully connected) neural layers. The second (and last) layer is a 10-way “softmax” layer, which means it will return an array of 10 probability scores (summing to 1).

To make the model ready for training, we need to pick three more things as part of the compilation step:

• An optimizer: The mechanism through which the model will update itself based on the data it sees and its loss function.
• A loss function: How the model will be able to measure its performance on the training data, and thus how it will be able to steer itself in the right direction.
• Metrics to monitor during training and testing: Here, we will only care about accuracy (the fraction of the images that were correctly classified).

# Listing 2.3 The compilation step
model.compile(optimizer='rmsprop',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

Before training, we will preprocess the data by reshaping it into the shap the model expects and scaling it so that all values are in the [0, 1] interval. Previously, our training images were stored in an array of shape (60000, 28, 28) of type uint8 with values in the [0, 255] interval. We will transform it into a float32 array of shape (60000, 28 * 28) with values between 0 and 1.

# Listing 2.4 Preparing the image data
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255

test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

We are now ready to train the model, which in Keras is done via a call to the model’s fit() method - we fit the model to its training data.

# Listing 2.5 "Fitting" the model
>>> model.fit(train_images, train_labels, epochs=5, batch_size=128)
Epoch 1/5
60000/60000 [==============================] - 4s 59us/sample - loss: 0.2542 - accuracy: 0.9261
Epoch 2/5
60000/60000 [==============================] - 3s 55us/sample - loss: 0.1038 - accuracy: 0.9690

Two quantities are displayed during training: the “loss” of the model over the training data, and the accuracy of the model over the training data. We quickly reach an accuracy of 0.989 (98.9%) on the training data.

Now that we have a trained model, we can use it to predict class probabilities for new difits - images that weren’t part of the training data, like those from the test set.

# Listing 2.6 Using the model to make predictions
>>> test_digits = test_images[0:10]
>>> predictions = model.predict(test_digits)
>>> predictions[0]
array([2.2380e-08, 2.6903e-10, 1.0881e-06, 1.0233e-05, 1.0663e-10, 1.0733e-08, 1.2383e-13, 9.9998e-01, 1.0517e-07, 1.0191e-06], dtype=float32)
>>> predictions[0].argmax() # or np.argmax(predictions[0])
7
>>> predictions[0][7]
0.99997973
>>> test_labels[0]
7

Each number of index i in predictions[0] is the model’s “confidence” that the digit input is i. The model thinks that the digit in test_digits[0] is a 7 with an accuracy of 99.9%.

On average, how good is our model at classifying such never-before-seen digits? Let’s check:

# Listing 2.7 Evaluating the model on the test data
>>> test_loss, test_acc = model.evaluate(test_images, test_labels)
>>> print(f'test_acc: {test_acc}')
test_acc: 0.9791

Our test set accuracy turns out to be 97.9% - that’s quite a bit lower than the training set accuracy. This gap between training accuracy and test accuracy is an example of overfitting, the fact that machine learning models tend to perform worse on new data than on their training data. Overfitting is a central topic in chapter 3.

You just saw how you can build and train a neual network to classify handwritten digits in less than 15 lines of Python code. Next you will learn about tensors, the data-storing objects going into the model; tensor operations, which layers are made of; and gradient descent, which allows your model to learn from its training examples.

2.2 Data representations for neural networks

In the previous example, we started from data stored in multidimensional NumPy arrays, also called tensors. In general, all current machine-learning systems use tensors as their basic data structure. Tensors are fundamental to the field - so fundamental that Google’s TensorFlow was named after them.

At its core, a tensor is a container for data - usually numerical data. So, it’s a container for numbers. You may be already familiar with matrices, which are rank-2 tensors: tensors are a generalization of matrices to an arbitrary number of dimensions (note that in the context of tensors, a dimension is often called an axis).

2.2.1 Scalars (rank-0 tensors)

A tensor that contains only one number is called a scalar (or scalar tensor, or rank-0 tesnsor, 0D tensor). In NumPy, a float32 or float64 number is a scalar tensor (or scalar array).

You can display the number of axis of a NumPy tensor via the ndim attribute; a scalar tensor has 0 axes(ndim == 0). The number of axes of a tensor is also called its rank. Here’s a NumPy scalar:

>>> import numpy as np
>>> x = np.array(12)
>>> x
array(12)
>>> x.ndim
0

2.2.2 Vectors (rank-1 tensors)

An array of numbers is called a vector, or rank-1 tensor, or 1D tensor. A rank-1 tensor is said to have exactly one axis. Following is a NumPy vector:

>>> x = np.array([12, 3, 6, 14, 7])
>>> x
array([12, 3, 6, 14, 7])
>>> x.ndim
1

This vector has five entries and so is called a 5-dimensional vector. Don’t confuse a 5D vector with a 5D tesnor! A 5D vector has only one axis and has five dimensions along its axis, whereas a 5D tensor has five axis (and may have any number of dimensions along each axis). Dimensionality can denote either the number of entries along a specific axis (as in the case of our 5D vector) or the number of axes in a tensor (such as a 5D tensor), which can be confusing at times. In the latter case, it’s technically more correct to talk about a tensor of rank 5 (the rank of a tensor being the number of axes), but the ambiguous notation 5D tensor is common regardless.

2.2.3 Matrices (rank-2 tensors)

An array of vectors is a matrix, or rank-2 tensor, or 2D tensor. A matrix has two axes (often referred to as rows and columns). You can visually interpret a matrix as a rectangular grid of numbers. This is a NumPy matrix:

>>> x = np.array([[5, 78, 2, 34, 0],
...               [6, 79, 3, 35, 1],
...               [7, 80, 4, 36, 2]])
>>> x.ndim
2
>>> x.shape
(3, 5)

The entries from the first axis are called the rows, and the entries from the second axis are called the columns. In the previous example, [5, 78, 2, 34, 0] is the first row of x, and [5, 6, 7] is the first column.

2.2.4 Rank-3 and higher-rank tensors

If you pack such matricies in a new array, you obtain a rank-3 tensor (or 3D tensor) which you can visually interpret as a cube of numbers. Following is a NumPy rank-3 tensor:

>>> x = np.array([[[5, 78, 2, 34, 0],
...                 [6, 79, 3, 35, 1],
...                 [7, 80, 4, 36, 2]],
...                [[5, 78, 2, 34, 0],
...                 [6, 79, 3, 35, 1],
...                 [7, 80, 4, 36, 2]],
...                [[5, 78, 2, 34, 0],
...                 [6, 79, 3, 35, 1],
...                 [7, 80, 4, 36, 2]]])
>>> x.ndim
3
>>> x.shape
(3, 3, 5)

By packing rank-3 tensors in an array, you can create a rank-4 tensor, an so on. In deep learning, you’ll generally manipulate tensors with ranks 0 to 4, although you may go up to 5 if you process video data.

2.2.5 Key attributes

A tensor is defined by three key attributes:

• Number of axes (rank): For instance, a rank-3 tensor has three axes, and a matrix has two axes. This is also called the tensor’s ndim in Python libraries such as NumPy or TensorFlow.
• Shape: This is a tuple of integers that describes how many dimensions the tensor has along each axis. For instance, the previous matrix example has shape (3, 5), and the rank-3 tensor example has shape (3, 3, 5). A vector has a shape with a single element, such as (5,), whereas a scalar has an empty shape, ().
• Data type(usually called dtype in Python libraries): This is the type of data contained in the tensor; for instance, a tensor’s type could be float16, float32, float64, uint8, and so on. In TensorFlow, you are also likely to come across string tensors.

To make this more concrete, let’s look back at the data we processed in the MNIST example. First, we load the MNIST dataset:

from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

Next we display the number of axes of the tensor train_images, the ndim attribute:

>>> print(train_images.ndim)
3

Here’s the shape of the train_images tensor:

>>> print(train_images.shape)
(60000, 28, 28)

So what we have here is rank-3 tensor of 8-bit integers. More precisely, it’s an array of 60000 matrices of 28x28 integers. Each such matrix is a grayscale image, with coefficients between 0 and 255.

Let’s display the fourth digit in rank-3 tensor, using the Matplotlib library( a well known Python data visualization library which comes preinstalled in Colab):

# Listing 2.8 Displaying the fourth digit
import matplotlib.pyplot as plt
digit = train_images[4]
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()

Naturally the corresponsin label is integer 9:

>>> train_labels[4]
9

2.2.6 Manipulating tensors in NumPy

In the previous example, we selected a specific digit alongside the first axis using the syntax train_images[i]. Selecting specific elements in a tensor is called tensor slicing. Let’s look at the tensor-slicing operations you can do on NumPy arrays.

The following example selects digits #10 to #100 (#100 isn’t included) and puts them in an array of shape (90, 28, 28):

>>> my_slice = train_images[10:100]
>>> print(my_slice.shape)
(90, 28, 28)

It’s equivalent to this more detailed notation, which specifies a start index and a stop index for the slice along each tensor axis. Note that : is equivalent to selecting the entire axis:

>>> my_slice = train_images[10:100, :, :]  # Equivalent to the previous example
>>> my_slice.shape
(90, 28, 28)
>>> my_slice = train_images[10:100, 0:28, 0:28]  # Also equivalent to the previous example
>>> my_slice.shape
(90, 28, 28)

In general, you may select between any two indices along each tensor axis. For instance, to select 14x14 pixels in the bottom-right corner of all images, you do this:

>>> my_slice = train_images[:, 14:, 14:]

It’s also possible to use negative indices. Much like negative indices in Python lists, they indicate a position relative to the end of the current axis. In order to crop the images to patches of 14x14 pixels centered in the middle, you do this:

>>> my_slice = train_images[:, 7:-7, 7:-7]

2.2.7 The notion of data batches

In general, the first axis (axis 0) in all data tensors will be the samples axis (sometimes called the samples dimension). In the MNIST example, samples are images of digits.

In addition, deep-learning models don’t process an entire dataset at once; rather, they break the data into small batches. Concretely, here’s one batch of our MNIST digits, with batch size of 128:

>>> batch = train_images[:128]

And here’s the next batch:

>>> batch = train_images[128:256]

And the nth batch:

>>> batch = train_images[128 * n:128 * (n + 1)]

When considering such a batch tensor, the first axis (axis 0) is called the batch axis or batch dimension. This is a term you will frequently encounter when using Keras and other deep-learning libraries.

2.2.8 Real-world examples of data tensors

Let’s make data tensors more concrete with a few examples similar to what you’ll encounter later. The data you’ll manipulate will almost always fall into one of the following categories:

• Vector data: Rank-2 tensors of shape (samples, features), where each sample is a vector of features. This is the most common case.
• Timeseries data or sequence data: Rank-3 tensors of shape (samples, timesteps, features), where each sample is a sequence(of length timesteps) of feature vectors.
• Images: Rank-4 tensors of shape (samples, height, width, channels), where each pixel is represented by a vector of values(channels)
• Video: Rank-5 tensors of shape (samples, frames, height, width, channels) where each sample is a sequence (of length frames) of images.

2.2.9 Vector data

This is one of the most common cases. In such a dataset, each single data point can be encoded as a vector, and thus a batch of data will be encoded as a rank-2 tensor(that is, an array of vectors), where the first axis is the samples axis and the second axis is the features axis.

Let’s take a look at two examples:

• An actuarial dataset of people, where we consider each person’s age, gender, and income. Each person can be characterized as a vector of 3 values, and thus an entire dataset of 100,000 people can be stored in a rank-2 tensor of shape (100000, 3).

• A dataset of text documents, where we represent each document by the counts of how many times each word appears in it (out of a dictionary of 20,000 common words). Each document can be encoded as a vector of 20,000 values (one count per word in the dictionary), and thus an entire dataset of 500 documents can be stored in a tensor of shape (500, 20000).

Generally the shape of rank-2 tensor is (samples, features).

2.2.10 Timeseries data or sequence data

Whenever time matters in your data ( or the notion of sequence order), it makes sense to store it in a rank-3 tensor with an explicitly time axis. Each sample can be encoded as a sequence of vectors (a rank-2 tesnor), and thus a batch of data will be encoded as a rank-3 tensor.

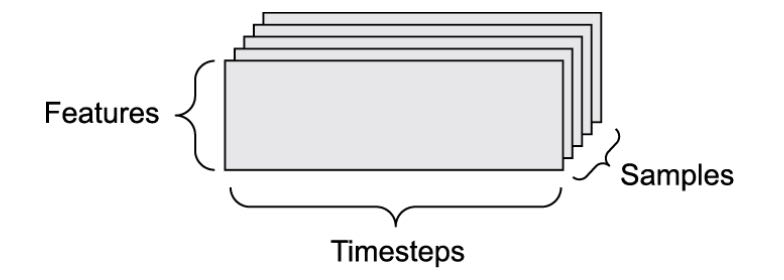
The time axis is always the second axis (axis of index 1), by convention. Let’s look at a few examples:

• A dataset of stock prices. Every minute, we store the current price of the stock, the highest price in the past minute, and the lowest price in the past minute. Thus every minute is encoded as a 3D vector, an entire day of trading is encoded as a matrix of shape (390, 3) (there are 390 minutes in a trading day), and 250 days’ worth of data can be stored in a rank-3 tensor of shape (250, 390, 3). Here, each sample would be one day’s worth of data.

• A dataset of tweets, where we encode each tweet as a sequence of 280 characters out of an alphabet of 128 unique characters. In this setting, each character can be encoded as a binary vector of size 128 (an all-zeros vector except for a 1 at the index corresponding to the character). Then each tweet can be encoded as a rank-2 tensor of shape (280, 128), and a dataset of 1 million tweets can be stored in a tensor of shape (1000000, 280, 128).

Generally the shape of rank-3 tensor is (samples, timesteps, features).

2.2.11 Image data

Images typically have three dimensions: height, width, and color depth. Although grayscale images( like our MNIST) have only a single color channel and could thus be stored in a rank-2 tensor, by convention image tensors are always rank-3, with a one-dimensional color channel for grayscale images. A batch of 128 grayscale images of size 256x256 could thus be stored in a tensor of shape (128, 256, 256, 1), and a batch of 128 color images could be stored in a tensor of shape (128, 256, 256, 3).

A rank-4 image data tensor figure:

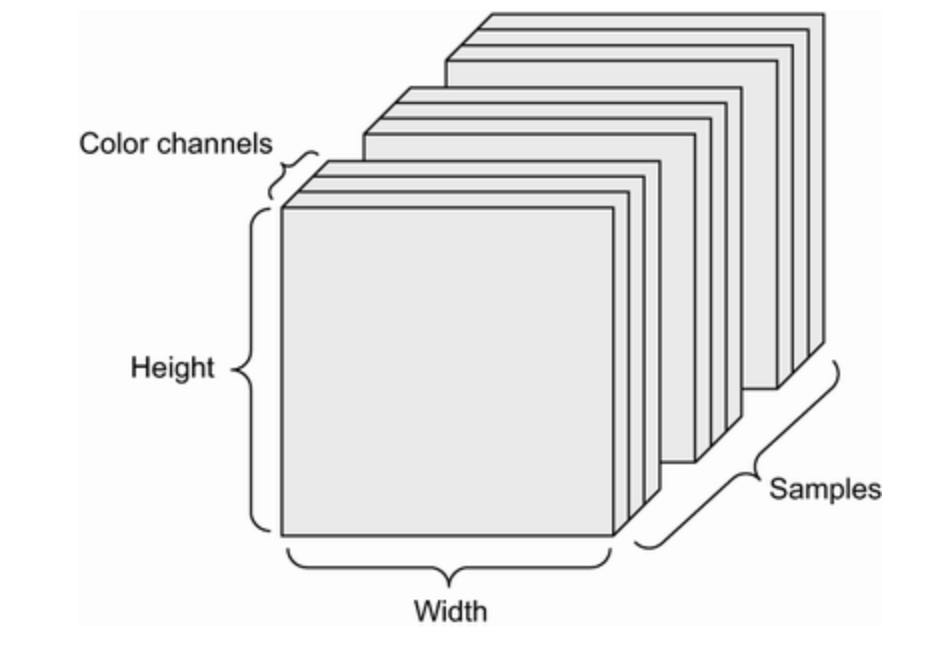
There are two conventions for shapes of image tensors: the channels-last conventions (which is a standard in TensorFlow) and the channels-first convention (which is incresingly falling out of favor).

Generally the shape of rank-4 tensor is (samples, height, width, channels).

2.2.12 Video data

Video data is one of the few types of real world data for which you’ll need rank-5 tensors. A video can be understood as a sequence of frames, where each frame is a color image. Because each frame can be stored in a rank-3 tensor (height, width, channels), a sequence of frames can be stored in a rank-4 tensor (frames, height, width, channels), and thus a batch of different videos can be stored in a rank-5 tensor of shape (samples, frames, height, width, channels).

For instance, a 60-second, 144x256 YouTube video clip sampled at 4 frames per second would have 240 frames. A batch of four such video clips would be stored in a tensor of shape (4, 240, 144, 256, 3). That’s a total of 106,168,320 values! If the dtype of the tensor was float32, then each value would be stored in 32 bits, so the tensor would represent 405MB. Heavy! Videos you encounter in real life won’t be this large, but this gives you an idea of what working with video data looks like.

Generally the shape of rank-5 tensor is (samples, frames, height, width, channels).

2.3 The gears of neural networks: tensor operations

Much as computer program can be ultimately reduced to a small set of binary operations on binary inputs (AND, OR, NOR, and so on), all transformations learned by deep neural networks can be reduced to a handful of tensor operations applied to tensors of numeric data. For instance, it’s possible to add tensors, multiply tensors, and so on.

In our initial example, we built our model by stacking Dense layers on top of each other. A Keras layer instance looks like this:

keras.layers.Dense(512, activation='relu')

This layer can be interpreted as a function, which takes as input a matrix and returns another matrix - a new representation for the input tensor. Specifically, the function is as follows (where W is a matrix and b is a vector, both attributes of the layer):

output = relu(dot(input, W) + b)

Let’s unpack this. We have three tensor operations here:

• A dot product (dot) between the input tensor and a tensor named W.
• An addition (+) between the resulting 2D tensor and a vector b.
• A relu operation. relu(x) is max(x, 0); “relu” stands for “rectified linear unit”.

Note: Instead of mathematical operations, we will be using short Python code snippets to explain the concepts. So we’ll use NumPy and TensorFlow code throughout.

2.3.1 Element-wise operations

The relu operation and addition are element-wise operations: operations that are applied independently to each entry in the tensors being considered. This means these operations are highly amenable to massively parallel implementations (vectorized implementations, a term that comes from the vector processor supercomputer architecture from the 1970s).

If you want to write a naive Python implementation of an element-wise relu operation, you could use a for loop:

def naive_relu(x):
    assert len(x.shape) == 2  # x is a rank-2 NumPy tensor
    x = x.copy()  # Avoid overwriting the input tensor
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] = max(x[i, j], 0)
    return x

You can do the same for addition:

def naive_add(x, y):
    assert len(x.shape) == 2  # x and y are rank-2 NumPy tensors
    assert x.shape == y.shape
    x = x.copy()  # Avoid overwriting the input tensor
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] += y[i, j]
    return x

On the same principle, you can do element-wise multiplication, subtraction, and so on.

In practice, when dealing with NumPy arrays, these operations are available as well-optimized built-in NumPy functions, which themselves delegate the heavy lifting to a Basic Linear Algebra Subprograms (BLAS) implementation if you have one installed, which you should. BLAS are low-level, highly parallel, efficient tensor-manipulation routines that typically implemented in Fortran or C.

So, in NumPy, you can do the following element-wise operation, and it will be blazing fast:

import numpy as np
z = x + y  # Element-wise addition
z = np.maximum(z, 0.)  # Element-wise relu

Let’s actually time the difference:

import time

x = np.random.random((20, 1000))
y = np.random.random((20, 1000))

t0 = time.time()
for _ in range(1000):
    z = x + y
    z = np.maximum(z, 0.)
print('Took: {0:.2f} seconds'.format(time.time() - t0))

This takes 0.02seconds. Meanwhile the naive version takes a stunning 2.45seconds. That’s a 100x difference!

t0 = time.time()
for _ in range(1000):
    z = naive_add(x, y)
    z = naive_relu(z)
print('Took: {0:.2f} seconds'.format(time.time() - t0))

Likewise, when running TensorFlow code on a GPU, element-wise operations are executed via fully vectorized C implementations that leverage the highly parallelized architecture of the GPU, making them very fast.

2.3.2 Broadcasting

Our earlier naive implementation of naive_add only supports the addition of rank-2 tensors with identical shapes. But in the Dense layer introduced earlier, we added a rank-2 tensor with a vector. What happens with addition when the shapes of the two tensors being added differ?

When possible, and if there’s no ambiguity, the smaller tensor will be broadcasted to match the shape of the larger tensor. Broadcasting consists of two steps:

1. Axes (called broadcast axes) are added to the smaller tensor to match the ndim of the larger tensor.
2. The smaller tensor is repeated alongside these new axes to match the full shape of the larger tensor.

Let’s look at a concrete example. Consider X with shape (32, 10) and y with shape (10,).

import numpy as np
x = np.random.random((32, 10))  # X is a random matrix with shape (32, 10)
y = np.random.random((10,))  # y is a random vector with shape (10,)

First, we add an empty first axis to y, whose shape becomes (1, 10).

y = np.expand_dims(y, axis=0)  # The shape of y is now (1, 10)

Then, we repeat y 32 times alongside this new axis, so that we end up with a tensor Y with shape (32, 10), where Y[i, :] == y for all i in range (0, 32).

y = np.concatenate([y] * 32, axis=0)  # Repeat y 32 times along axis 0 to obtain Y, which has a shape of (32, 10)

At this point, you can proceed to add X and y, because they have the same shape.

In terms of implementation, no new rank-2 tensor is created, because that would be terribly inefficient. The repetition operation is entirely virtual: it happens at the algorithmic level rather than at the memory level. But thinking of the vector being repeated 10 times alongside a new axis is a helpful mental model. Here’s what the code looks like:

def naive_add_matrix_and_vector(x, y):
    assert len(x.shape) == 2  # x is a rank-2 NumPy tensor
    assert len(y.shape) == 1  # y is a NumPy vector
    assert x.shape[1] == y.shape[0]
    x = x.copy()  # Avoid overwriting the input tensor
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] += y[j]
    return x

With broadcasting, you can generally perform element-wise operations that take two inputs tensor if one tensor has shape (a, b, ... n, n+1, ... m) and the other has shape (n, n+1, ... m). The broadcasting will then automatically happen for axes a through n-1.

The following example applies the element-wise maximum operation to two tensors of different shapes via broadcasting:

import numpy as np
x = np.random.random((64, 3, 32, 10))  # x is a random tensor with shape (64, 3, 32, 10)
y = np.random.random((32, 10))  # y is a random tensor with shape (32, 10)

z = np.maximum(x, y)  # The output z has shape (64, 3, 32, 10) like x

2.3.3 Tensor product

The tensor product or dot product (not to be confused with an element-wise product, the * operator) is one of the most common, most useful tensor operations.

In Numpy, a tensor product is done using the np.dot function (because the mathematical notation for tensor product is usually a dot).

x = np.random.random((32,))  # x is a random vector with shape (32,)
y = np.random.random((10,))  # y is a random vector with shape (10,)
z = np.dot(x, y)  # The output z is a scalar

In mathematical notation, you would note the operation as z = x . y.

Mathematically, what does the dot operation do? Let’s start with the dot product of two vectors x and y. It’s computed as follows:

def naive_vector_dot(x, y):
    assert len(x.shape) == 1  # x and y are NumPy vectors
    assert len(y.shape) == 1
    assert x.shape[0] == y.shape[0]
    z = 0.
    for i in range(x.shape[0]):
        z += x[i] * y[i]
    return z

You’ll have noticed that the dot product between two vectors is a scalar and that only vectors with the same number of elements are compatible for a dot product.

You can also take the dot product between a matrix x and a vector y, which returns a vector where the coefficients are the dot products between y and the rows of x. Here’s a naive implementation:

def naive_matrix_vector_dot(x, y):
    assert len(x.shape) == 2  # x is a NumPy matrix
    assert len(y.shape) == 1  # y is a NumPy vector
    assert x.shape[1] == y.shape[0]  # The first dimension of x must be the same as the 0th dimension of y
    z = np.zeros(x.shape[0])  # This operation returns a vector of 0s with the same shape as y
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            z[i] += x[i, j] * y[j]
    return z

You could also reuse the code we wrote previously, which highlights the relationship between a matrix-vector product and a vector product:

def naive_matrix_vector_dot(x, y):
    z = np.zeros(x.shape[0])
    for i in range(x.shape[0]):
        z[i] = naive_vector_dot(x[i, :], y)
    return z

Note that as soon as one of the two tensors has an ndim greater than 1, dot is not longer symmetric, which is to say that dot(x, y) isn’t the same as dot(y, x).

Of course, a dot product generalizes to tensors with an arbitrary number of axes. The most common applications may be the dot product between two matrices. You can take the dot product of two matrices x and y (dot(x, y)) if and only if x.shape[1] == y.shape[0]. The result is a matrix with shape (x.shape[0], y.shape[1]), where the coefficients are the vector products between the rows of x and the columns of y. Here’s a naive implementation:

def naive_matrix_dot(x, y):
    assert len(x.shape) == 2  # x and y are NumPy matrices
    assert len(y.shape) == 2
    assert x.shape[1] == y.shape[0]  # The first dimension of x must be the same as the 0th dimension of y
    z = np.zeros((x.shape[0], y.shape[1]))  # This operation returns a matrix of 0s with a specific shape
    for i in range(x.shape[0]):
        for j in range(y.shape[1]):
            row_x = x[i, :]
            column_y = y[:, j]
            z[i, j] = naive_vector_dot(row_x, column_y)
    return z

To understand the dot-product shape compatibility, it help to visualize the input and output tensors by aligning them as shown in the following figure:

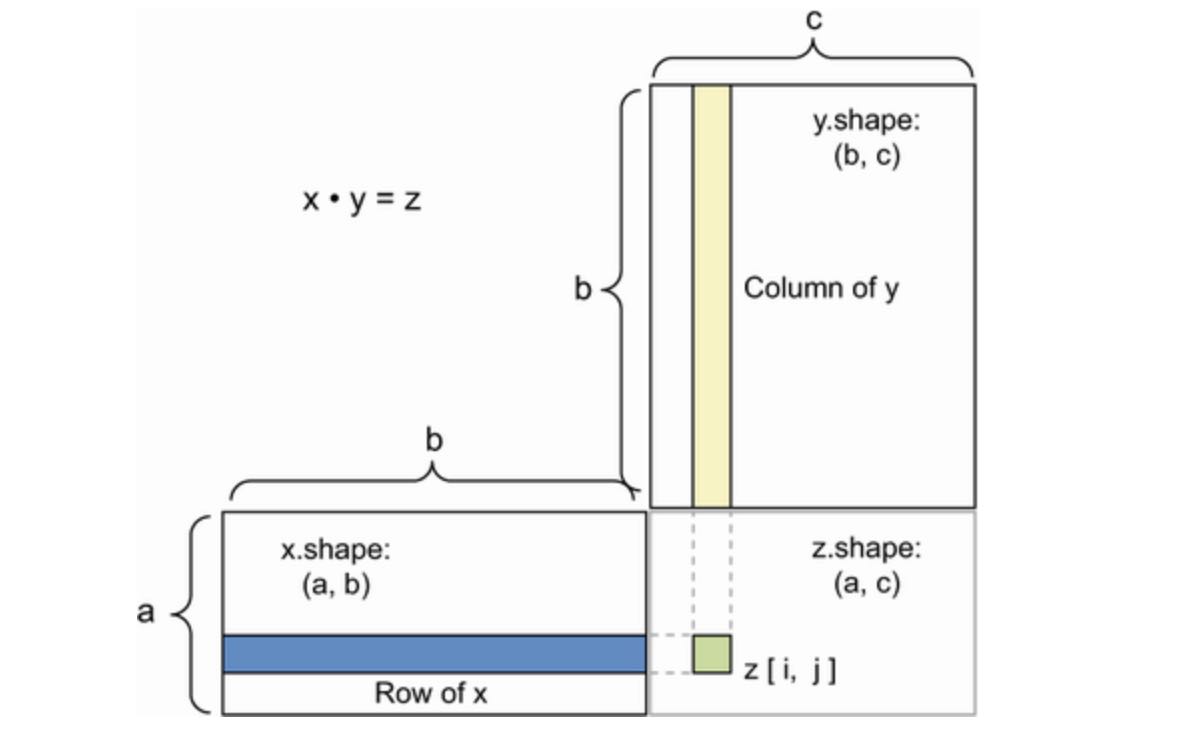
In the figure, x, y and z are pictured as rectangles(literal boxes of coefficients). Because the rows of x and the columns of y, it follows that the width of x must match the height of y. If you go on to develop a new machine learning algorithms, you’ll likely be drawing such diagrams often.

More generally, you can take the dot product between highr-dimensional tensors, following the same rules for shape compatibility as outlined earlier for the 2D case:

(a, b, c, d) . (d,) -> (a, b, c)
(a, b, c, d) . (d, e) -> (a, b, c, e)

2.3.4 Tensor reshaping

A third type of tensor operations that’s essential to understand is tensor reshaping. Although it wasn’t used in the Dense layers in our first neural network example, we used it when we preprocessed the digits data before feeding it into our model:

train_images = train_images.reshape((60000, 28 * 28))

Reshaping a tensor means rearranging its rows and columns to match a target shape. Naturally, the reshaped tensor has the same total number of coefficients as the initial tensor. Reshaping is best understood via simple examples:

>>> x = np.array([[0., 1.],
...               [2., 3.],
...               [4., 5.]])
>>> print(x.shape)
(3, 2)
>>> x = x.reshape((6, 1))
>>> x
array([[0.],
       [1.],
       [2.],
       [3.],
       [4.],
       [5.]])
>>> x = x.reshape((2, 3))
>>> x
array([[0., 1., 2.],
       [3., 4., 5.]])

2.3.5 Geometric interpretation of tensor operations

Because the contents of the tensors manipulated by tensor operations can be interpreted as coordinates of points in some geometric space, all tensor operations have a geometric interpretation. For instance, let’s consider addition. We will start with the following vector:

A = [0.5, 1]

It’s a point in 2D space.

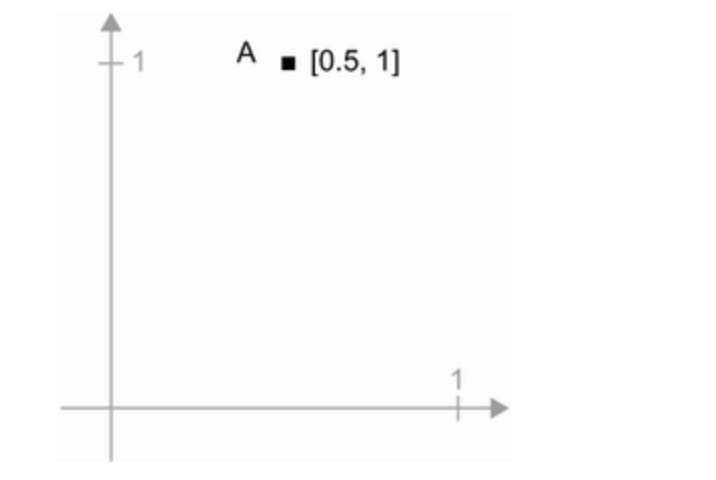
It’s common to picture a vector as an arrow linking the origin to the point.

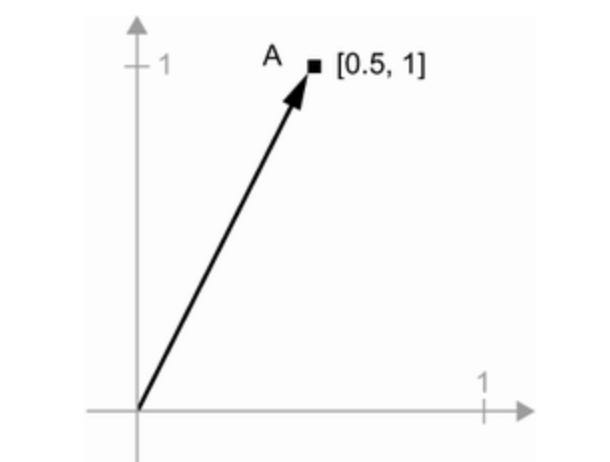
Let’s consider a new point, B = [1, 0.25], which we’ll add to the previous one. This is done geometrically by chaining together the vector arrows, with the resulting location being the vector representing the sum of the previous two vectors.

As you can see, adding a vector B to vector A represents the action of copying point A in a new location, whose distance and direction from the original point A is determined by the Vector B. If you apply the same vector addition to a group of points in the plane (an “object”), you would be creating a copy of the entire object in a new location. See the below figure:

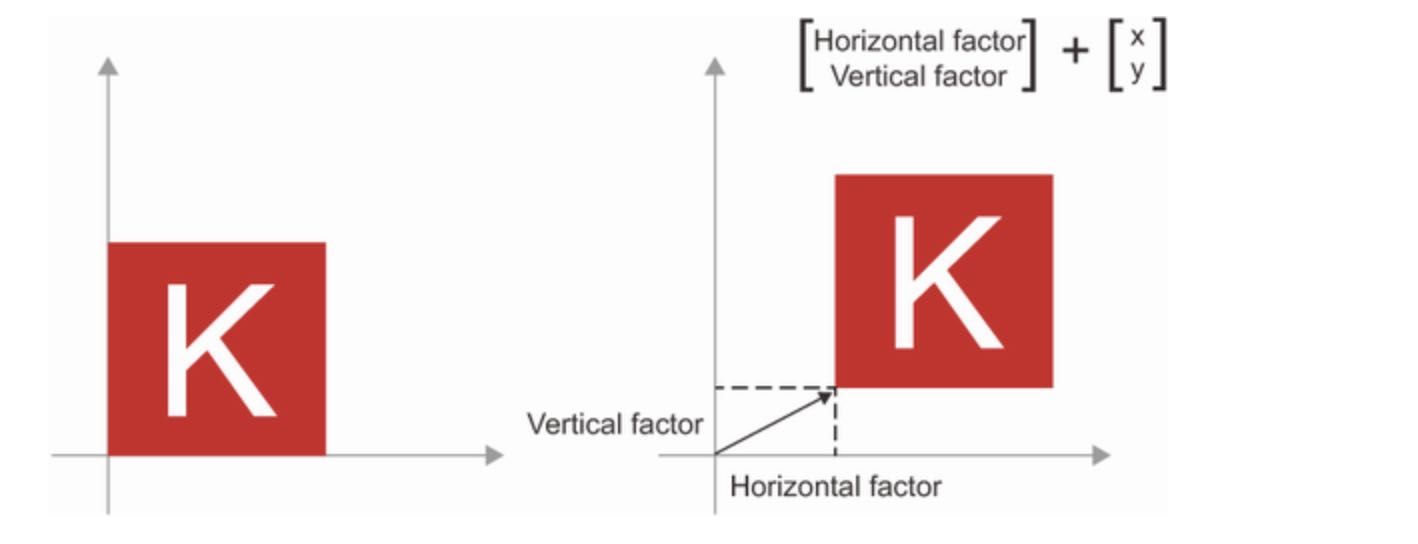
In general, elementary geometric operations such as translation, scaling, skewing, and so on can be expressed as tensor operations. Here are few examples:

• Translation: As you just saw, adding a vector to a point will move the point by a fixed amount in fixed direction. Applied to a set of points (such as 2D object), this is called a “translation”.

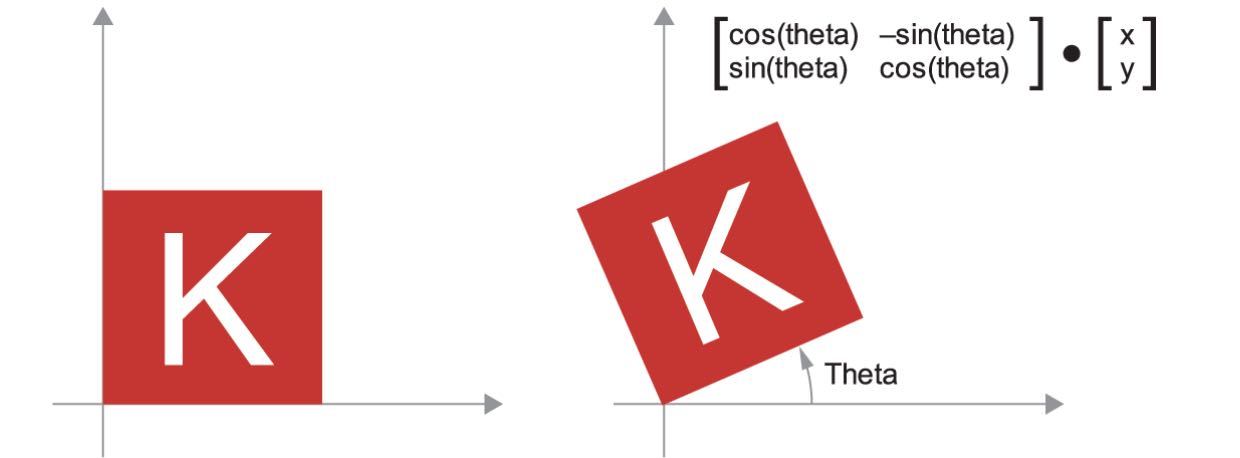
• Rotation: A counterclockwise rotation of a 2D vector by an angle theta can be achieved via a dot product with a 2x2 matrix R = [[cos(theta), -sin(theta)], [sin(theta), cos(theta)]].

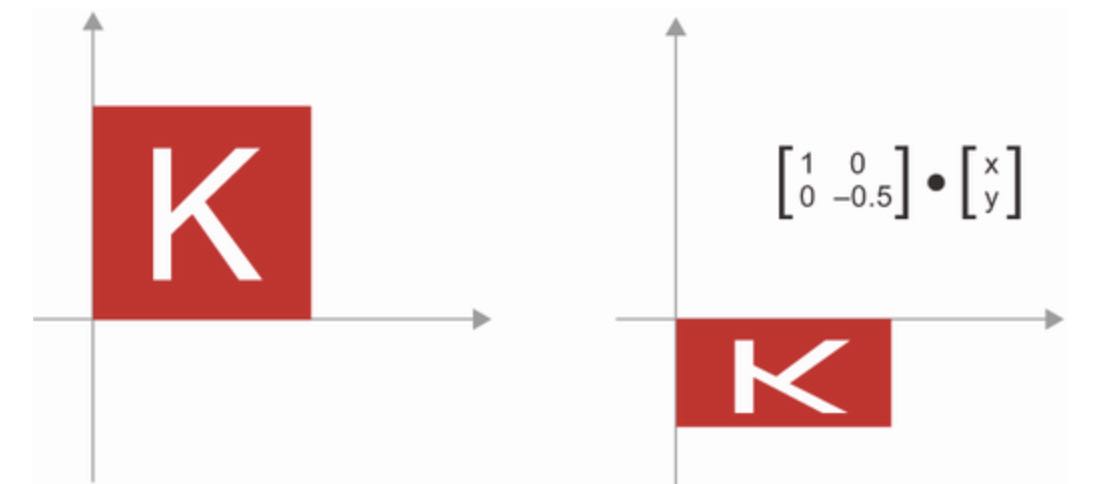
• Scaling: A vertical and horizontal scaling of the image can be achieved via a dot product with a 2x2 matrix S = [[horizontal_factor, 0], [0, vertical_factor]]. Note that such a matrix is called a “diagonal matrix”, because it only has non-zero coefficients in its diagonal, going from “left-top” to “right-bottom”.

• Linear transform: A dot product with an arbitrary matrix implements a linear transform. Note that scaling and rotation, listed previously, are by definition linear transforms.

• Affine transform: An affine transform is the combination of a linear transform (achieved via a dot product with some matrix) and a translation (achieved via a vector addition). As you have probably recognized, that’s exactly what the y = W.x + b computation does in a Dense layer! A Dense layer without an activation function is an affine layer.

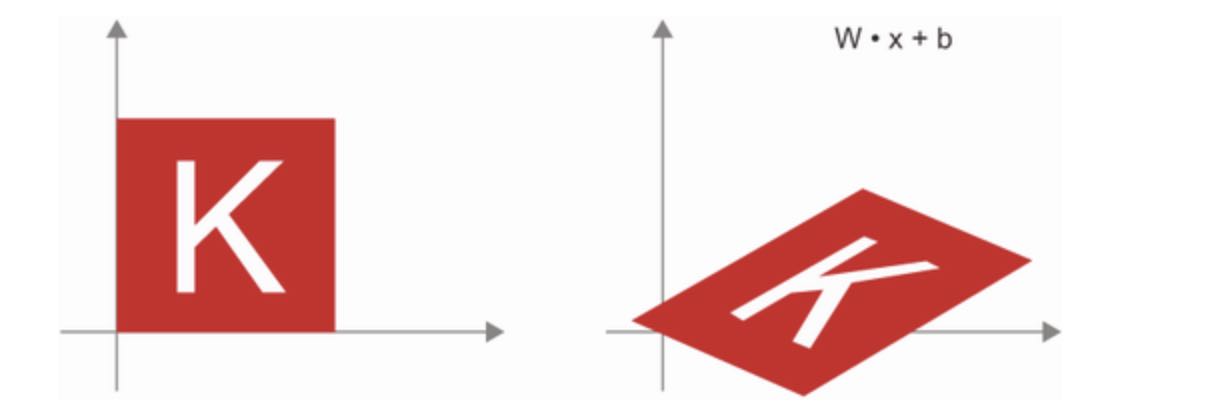
• Dense layer with relu activation: An important observation about affine transformation is that if you apply many of them repeateadly, you still end up with an affine transform (so you could have just applied that one affine transform in the first place). Let’s try it with two: affine2(affine1(x)) = W2.(W1.x + b1) + b2 = (W2.W1).x + W2.b1 + b2. As a consequence, a multilayer neural network made entirely of Dense layers without activations would be equivalent to a single Dense layer. This “deep” neural network would just be the linear model in disguise! This is why we need activation functions like relu to introduce non-linearity to the model. Thanks to activation functions, a chain of Dense layers can be made to implement very complex, non-linear geometric transformations, resulting in very rich hypothesis spaces for your deep neural networks. We will cover this idea more in detail in next chapter

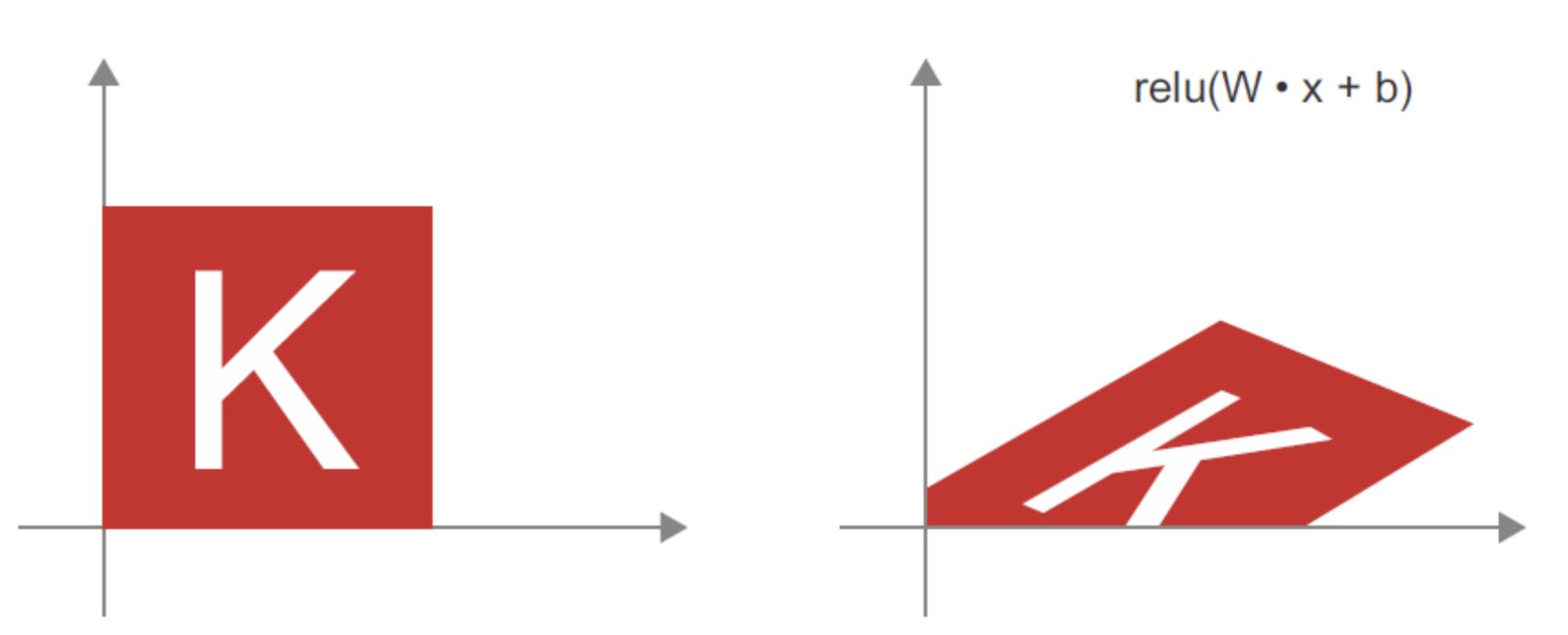
2.3.6 A geometric interpretation of deep learning

You just learned that neural networks consist entirely of chains of tensor operations and that these tensor operations are just simple geometric transformations of the input data. It follows that you can interpret a neural network as a very complex geometric transformation in a high-dimensional space, implemented via a series of simple steps.

In 3D, the following mentral image may prove useful. Imagine two sheets of colored paper: one red and one blue. Put one on top of the other. Now crumple them together into a small ball. That crumpled paper ball is your input data, and each sheet of paper is a class of data in a classification problem. What a neural network (or any other machine-learning model) is meant to do is figure out a transformation of the paper ball that would uncrumple it, so as to make the two classes separable again. With deep learning, this would be implemented as a series of simple transformations of the 3D space, such as those you could apply on the paper ball with your fingers, one movement at a time.

Uncrumpling paper balls is what machine learning is about: finding neat representations for complex, highly folded data manifolds in high-dimensional spaces (a manifold is a continuous surface, like our crumpled sheet of paper). At this point, you should have pretty good intuition as to why deep learning excels at this: it takes the approach of incrementally decomposing a complicated geometric transformation into a long chain of elementary ones, which is pretty much the strategy a human would follow to uncumple a paper ball. Each layer in a deep network applies a transformation that disentangles the data a little, a deep stack of layers makes tractable an extremely complicated disentanglement process.

2.4 The engine of neural networks: gradient-based optimization

As you saw in the previous section, each neural layer from our first model example transforms its input data as follows:

output = relu(dot(W, input) + b)

In this expression, W and b are tensors that are attributes of the layer. They’re called the weights or trainable parameters of the layer (the kernel and bias attributes, respectively). These weights contain the information learned by the model from exposure to training data.

Initially, these weight matrices are filled with small random values (a step called random initialization). Of course, there’s no reason to expect that relu(dot(W, input) + b), when W and b are random, will yield any useful representations. The resulting representations are meaningless - but they’re a starting point. What comes next is to gradually adjust these weights, based on a feedback signal. This gradual adjustment, also called training, is basically the learning that machine learning is all about.

This happens within what’s called a training loop, which works as follows:

1. Draw a batch of training samples x and corresponding targets y_true.
2. Run the model on x (a step called the forward pass) to obtain predictions y_pred.
3. Compute the loss of the model on the batch, a measure of the mismatch between y_pred and y_true.
4. Update the weights of the model to minimize the loss, a step called the backward pass (or backpropagation).

You eventually end up with a model that has very low loss on its training data: a low mismatch between predictions y_pred and expected targets y_true. The model has “learned” to map its inputs to correct targets.

Step 1 sounds easy enough - just I/O code. Step 2 and 3 are merely the application of a handful of tensor operations, so you could implement these steps in pure Python and NumPy. The difficult part is step 4: updating the model’s weights. Given an individual weight coefficient in the model, how can you compute whether the coefficient should be increased or decreased, and by how much?

One naive solution would be to freeze all weights in the model except the one scalar coefficient being considered, and try different values for this coefficient. Let’s say the initial value of the coefficient is 0.3. After the forward pass on a batch of data, the loss of the model on the batch is 0.5. If you change the coefficient’s value to 0.35 and rerun the forward pass, the loss increases to 0.6. But if you lower the coefficient to 0.25, the loss falls to 0.4. In this case, it seems that updating the coefficient by -0.05 would contribute to minimizing the loss. This would have to be repeated for all coefficients in the model.

But such an approach would be horribly inefficient, because you’d need to compute two forward passes (which are expensive) for every individual coefficient (of which there are many, often thousands and sometimes up to millions). Thankfully, there’s a much better approach: gradient descent.

Gradient descent is the optimization technique that powers modern neural networks. Here’s the gist of it. All of the functions used in our models(such as dot or +) transform their input in a smooth and continuous way: if you look at z = x + y, for instance, a small change in y only results in small change in z, and if you know the direction of change in y, you can infer the direction of the change in z. Mathematically, you can say these functions are differentiable. If you chain together such functions, the bigger function you obtain is still differentiable. In particular, this applies to the function that maps the model’s coefficients to the loss of the model on a batch of data: a small change in model coefficients results in a small, predictable change in the loss value. This enables you to use a mathematical operator called gradient to describe how the loss varies as you move the model’s coefficients in different directions. If you compute this gradient, you can use it to move the coefficients all at once in a single update, rather than one at a time.

2.4.1 What’s a derivative?

Consider a continuous, smooth function f(x) = y, mapping a real number x to a new real number y. We can use the following function as an example:

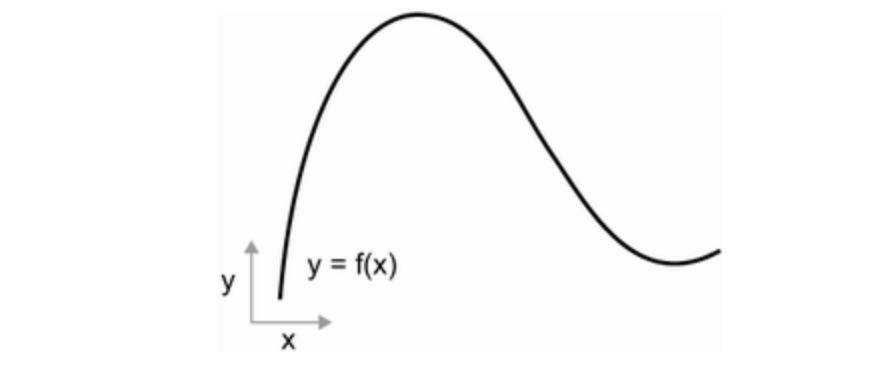
Because the function is continuous, a small change in x can only result in a small change in y - that’s the intution behind continuity. Let’s say you increase x by a small factor epsilon_x. This results in a small change epsilon_y change to y, as shown in the following figure:

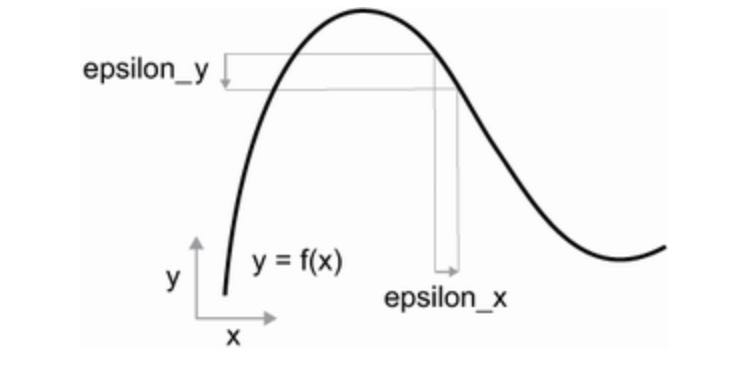
In addition, because the function is smooth (the curve doesn’t have any abrupt angles), when epsilon_x is small enough around a certain point p, it’s possible to approximate f as a linear function of slope a, so that epsilon_y becomes a * epsilon_x.

f(x + epsilon_x) = f(x) + a * epsilon_x

Obviously, the linear approximation is valid only when epsilon_x is small enough.

The slope a is called the derivative of f at point p. If a is negative, it means a small increase in x around p results in a decrease in f(x), and if a is positive, it means a small increase in x around p results in an increase in f(x). Further the absolute value of a tells you how quickly this increase or decrease will happen.

For every differentiable function f(x) (differentiable means “can be derived”: for example, smooth, continuous functions can be derived), there exist a derivative function f'(x), that maps values of x to the slope of local linear approximation of f in those points. For instance, the derivative of cos(x) is -sin(x), the derivative of f(x) = a * x is a, and the derivative of f(x) = x^2 is 2 * x.

[Commentary: This is powerful paragraph.]

Being able to derive functions is a very powerful tool when it comes to optimization. If you update x by a factor epsilon_x in order to minimize f(x), and you know the derivative of f, then your job is done: the derivative completely describes how f(x) evolves as you change x. If you want to reduce the value of f(x), you just need to movve x a little in the opposite direction from the derivative. This is the idea behind gradient descent.

2.4.2 Derivative of a tensor operation: the gradient

The function we were just looking at (y = f(x)) turned a scalar value x (i.e. rank-0 tensor) into another scalar value y: you could plot it as a curve in a 2D plane. Now imagine a function that turns a tuple of scalars (x, y) (i.e. rank-1 tensor) into a scalar value z: that would be a vector operation. (i.e. z = f(x, y)). You could plot it as a 2D surface in a 3D space (indexed by coordinates (x, y, z)). Likewise, you can imagine functions that take matrices(i.e. rank-2 tensors) as inputs, functions that take rank-3 tensors as inputs, etc.

The concept of derivation can be applied to any such function, as long as the surfaces they describe are continuous and smooth. The derivative of a tensor operation(or tensor function) is called a gradient. Gradients are just the generalization of the concept of derivatives to functions that take tensors as inputs. Remember, how for a scalar function, the derivative represents the local scope of the curve of the function? In the same way, the gradient of a tensor function represents the curvature of multidimensional surface described by the tensor function (i.e. the coefficients in matrix). It characterizes how the output of the function varies when its input parameters vary.

[Commentary: Only computers can solve/generate functions through this approach of calculating coefficients using the brute force method. This is the power of deep learning.]

Let’s look at an example grounded in machine learning. Consider:

• An input vector, x(a sample in a dataset)
• A matrix, W (the weights of the model)
• A target, y_true (what the model should learn to associate with x)
• A loss function, loss (how well the model is doing on a batch of data, given its weights)

You can use W to compute a target candidate y_pred and then compute the loss, or mismatch, between the target candidate y_pred and the target y_true.

y_pred = dot(W, x)  ## We use the model weights, W, to make prediction for x
loss_value = loss(y_pred, y_true)  ## We estimate how far off the prediction was

Now we would like to use gradients to figure out how to update W so as to make loss_value smaller. How can we do that?

Given fixed inputs x and y_true, the preceding operations can be interpreted as a function mapping values of W(the model weights) to loss values:

loss_value = f(W)  ## f describes the curve (or high-dimensional surface) formed by the loss values when `W` varies

Let’s say the current value of W is W0. Then the derivative of f at the point W0 is a tensor grad(loss_value, W0) with the same shape as W, where each coefficient grad(loss_value, W0)[i, j] indicates the direction and magnitude of the change in loss_value you would observe if you changed W0[i, j]. That tensor grad(loss_value, W0) is the gradient of f(W) at point W0, also called the gradient of loss_value with respect to W around W0.

Partial Derivatives: The tensor operation grad(f(W), W) (which takes as input a matrix W) can be expressed as a combination of scalar functions, grad_ij(f(W), w_ij), each of which would return the derivative of loss_value = f(W) with respect to the coefficient W[i, j] of W, assuming all other coefficients are constant, grad_ij is called the partial derivative of f with respect to W[i, j].

Concretely, what does grad(loss_value, W0) represent? You saw earlier that derivative of a function f(x) of a single coefficient can be interpreted as slope of the curve of f. Likewise, grad(loss_value, W0) can be interpreted as the tensor describing the direction of steepest ascent of loss_value = f(W) as well as the slope of this ascent. Each partial derivative describes the slope of f in a specific direction.

For this reason, in the much the same way that, for a function f(x), you can reduce the value of f(x) by moving x a little in the opposite direction from the derivative, with a tensor function f(W), you can reduce loss_value = f(W) by moving W in the opposite direction from the gradient: for example, W1 = W0 - step * grad(f(W0), W0) (where step is a small scaling factor). That means going against the direction of steepest ascent of f, which intuitively should put you lower on the curve. Note that the factor step is needed because grad(loss_value, W0) only approximates the curve when you are close to W0, so you don’t wan to get too far from W0.

2.4.3 Stochastic gradient descent

Given a differentiable function, it’s theoretically possible to find its minimum analytically: it’s known that a function’s minimum is a point where the derivative is 0, so all you have to do is find all the points where the derivatives goes to 0 and check for which of these points the function has the lowest value.

Applied to neural network, that means finding analytically the combination of weight values that yields the smallest possible loss function. This can be done by solving the equation grad(loss_value, W) = 0 for W. This is a polynomial equation of N variables, where N is the number of coefficients in the model. Although, it would be possible to solve the equation for N = 2 or N = 3, doing so is intractable for real neural networks, where the number of parameters is never less than a few thousand and often be several tens of millions.

Instead, you can use the four-step algorithm outlined at the beginning of previous section: modify the parameters little by little based on the current loss value for a random batch of data. Because you are dealing with a differentiable function, you can compute its gradient, which gives you an efficient way to implement step 4. If you update the weights in the opposite direction from the gradient, the loss will be a little less every time.

1. Draw a batch of training samples x and corresponding targets y_true.
2. Run the model on x to obtain predictions y_pred. This is called the forward pass.
3. Compute the loss of the model on the batch, a measure of the mismatch between y_pred and y_true.
4. Compute the gradient of the loss with regard to the model’s parameters (a backward pass). This is called the backward pass.
5. Move the parameters a little in the opposite direction from the gradient - for example W -= learning_rate * gradient, thus reducing the loss on the batch a bit. The learning rate would be a scalar factor modulating the “speed” of the gradient descent process.

What we just described is called mini-batch stochastic gradient descent (mini-batch SGD). The term stochastic refers to the fact that each batch of data is drawn at random (stochastic is a scientific synonym of random). The following figure illustrates what happens in 1D, when the model has only one parameter and you have only one training sample:

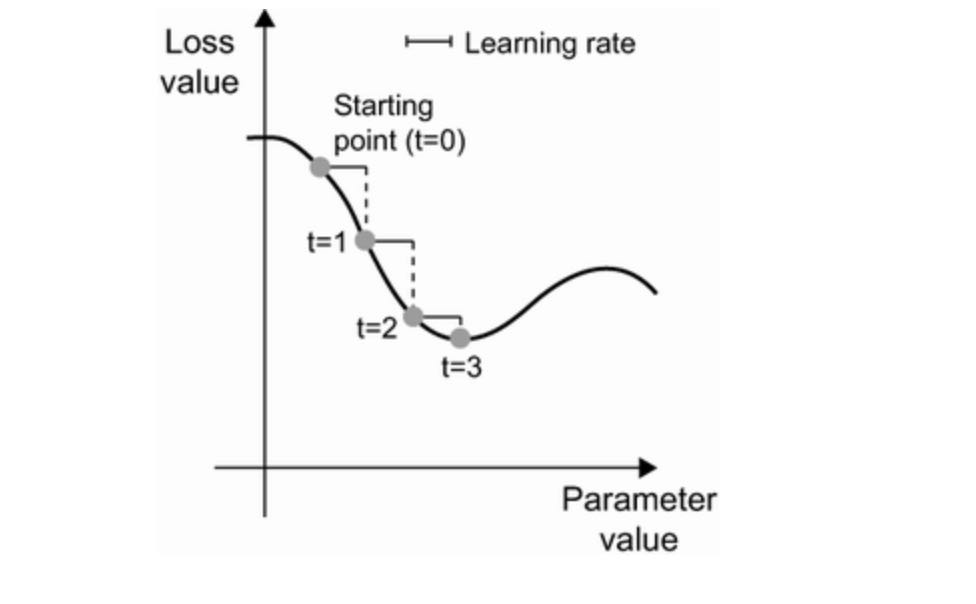
As you can see, intuitively, it’s important to pick a reasonable value for the learning_rate factor. If it’s too small, the descent down the curve will take many iterations, and it could get stuck in a local minimum. If learning_rate is too large, your updates may end up taking you to completely random locations on the curve.

Note that a variant of mini-batch SGD algorithm would be to draw a single sample and target at each iteration, rather than drawing a batch of data. This is called true SGD (as opposed to mini-batch SGD). Alternatively, going to the opposite extreme, you could run every step on all data available, which is called batch gradient descent. Each update in Batch Gradient Descent would then be more accurate, but far more expensive. The efficient compromise is to use mini-batches of reasonable size.

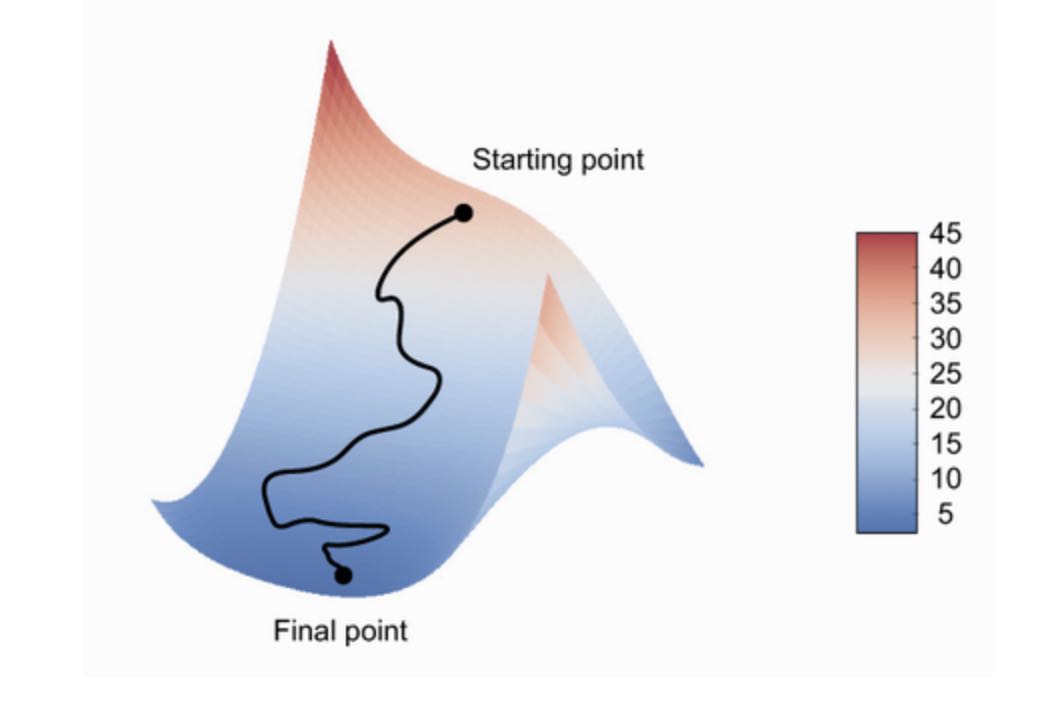
Although the above figure illustrates gradient descent in a 1D parameter space, in practice, you will use gradient descent in highly dimensional spaces: every weight coefficient in a neural network is a free dimension in the space, and there may be tens of thousands or even millions of them. To help you build intuition about loss surfaces, you an also visualize gradient descent along a 2D loss surface, as shown in the following figure. But you can’t possibly visualize what the actual process of training a neural network looks like, because it takes place in a 10,000+ dimensional space. As such, it’s good to keep in mind that the intuitions you develop through these low dimensional representations may not always be accurate in practice. This has historically been a source of issues in deep learning research.

Additionally, there exists multiple variants of SGD that differ by taking into account previous weight updates when computing the next weight update, rather than just looking at the current value of the gradients. There is for instance, SGD with momentum, as well as Adagrad, RMSprop, and several others. Such variants are known as optimization methods or optimizers. In particular, the concept of momentum, which is used in many of these variants, deserves your attention. Momentum addresses two issues with SGD: convergence speed and local minima. Consider the following figure, which shows the curve of a loss as a function of a model parameter.

As you can see, around a certain parameter value, there is a local_minimum: around that point, moving left would result in the loss increasing, but so would moving right. If the parameter under consideration were being optimized via SGD with a small learning rate, the optimization process could get stuck at the local minimum instead of making its way to the global minimum.

You can avoid such issues by using momentum, which draws inspiration from physics. A useful mental image here is to think of the optimization process as a small ball rolling down the loss curve. If it has enough momentum, the ball wouldn’t get stuck in a ravine and will end up at the global minimum. Momentum is implemented by moving the ball at each step based not only on the current slope value (current acceleration) but also on the current velocity (resulting from past acceleration). In practice, this means updating the parameter w based on not only the current gradient value, but also the previous parameter update. The formula for updating the parameter w would then look as follows:

past_velocity = 0.
momentum  = 0.1  ## Constant momentum factor
while loss > 0.01:
    w, loss, gradient = get_current_parameters()
    velocity = past_velocity * momentum + learning_rate * gradient
    w = w + momentum * past_velocity - learning_rate * gradient
    past_velocity = velocity
    update_parameter(w)

2.4.4 Chaining Derivatives: The Backpropagation Algorithm

In the preceding algorithm, we casually assumed that because a function is differentiable, we can easily compute its gradient. But is that true? How can we compute the gradient of complex expressions in practice? In the two-layer model we started the chapter with, how can we get the gradient of the loss with regard to the weights? That’s where the Backpropagation algorithm comes in.

THE CHAIN RULE:

Backpropagation is a way to use the derivatives of simple operations (such as addition, relu, or tensor product) to easily compute the gradient of arbitrarily complex combinations of these atomic operations. Crucially, a neural network consists of many tensor operations chained together, each of which has a simple, known derivative. For instance, the model defined in listing 2.2( with 512, and 10 parameters) can be expressed as a function parameterized by variables W1, b1, W2, and b2(belonging to the first and second Dense layers respectively), involving the atomic operations dot, relu, softmax and +, as well as our loss function loss, which are all easily differentiable:

loss_value = loss(y_true, softmax(dot(relu(dot(inputs, W1) + b1), W2) + b2))

Calculus tells us that such a chain of functions can be derived using the chain rule:

Consider two functions f and g, and a function fg such that fg(x) = f(g(x)):

def fg(x):
    x1 = g(x)
    y = f(x1)
    return y

Then the chain rule states that grad(y, x) == grad(y, x1) * grad(x1, x). This enables you to compute the derivative of fg as long as you know the derivatives of f and g. The chain rule is named as it is because when you add more intermediate functions, it starts looking like a chain:

def fghj(x):
    x1 = j(x)
    x2 = h(x1)
    x3 = g(x2)
    y = f(x3)
    return y

grad(y, x) == (grad(y, x3) * grad(x3, x2) * grad(x2, x1) * grad(x1, x))

Applying the chain rule to the computation of the gradient values of a neural network gives rise to an algorithm called Backpropagation. Lets see how that works concretely.

AUTOMATIC DIFFERENTIATION WITH COMPUTATION GRAPHS:

A useful way to think about backpropagation is in terms of computation graphs. A computation graph is the data structure at the heart of TensorFlow and the deep learning revolution in general. It’s a directed acyclic graph of operations - in our case, tensor operations. The following figure shows the graph representation of our first model:

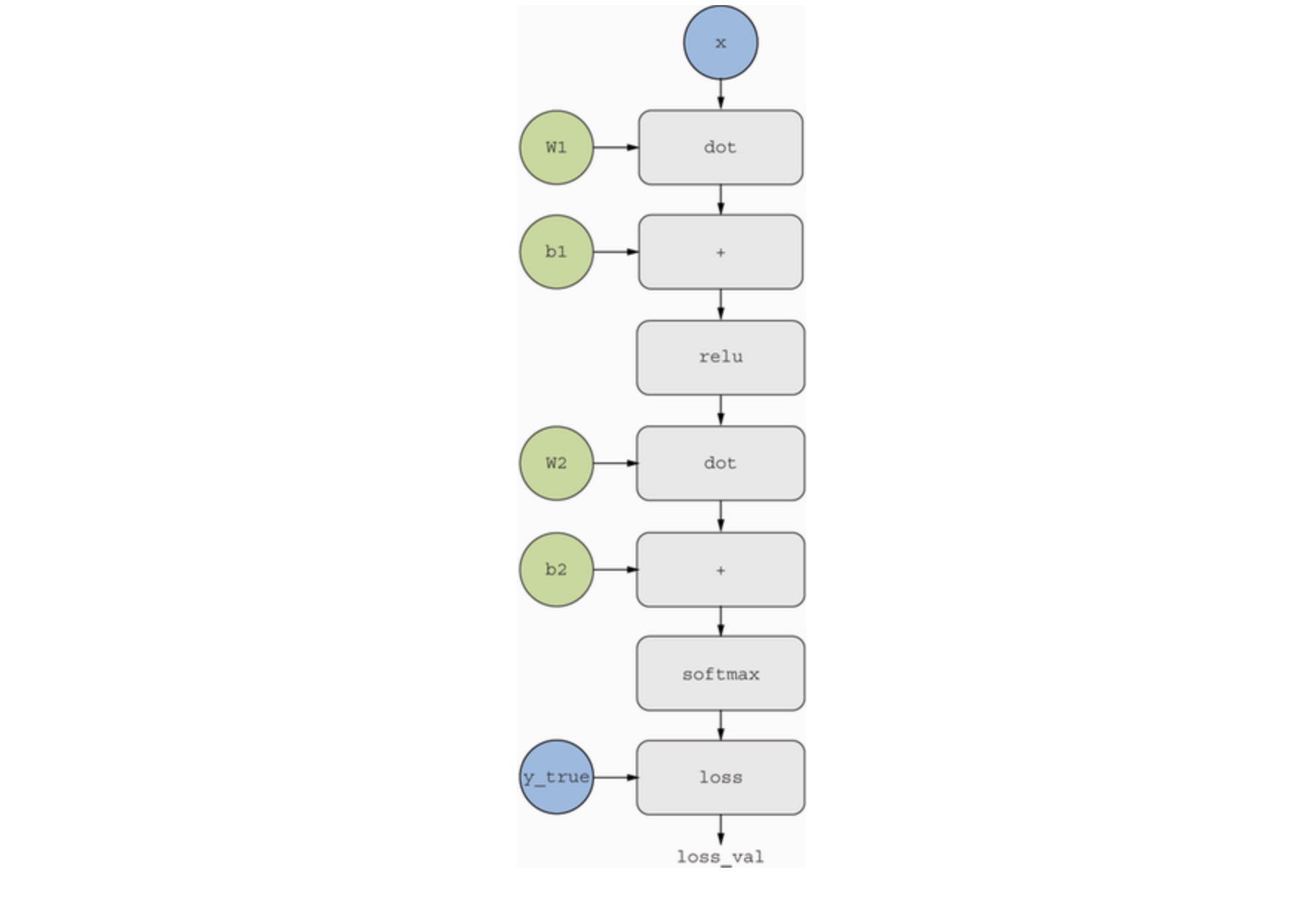
Computation graphs have been an extremely successful abstraction in computer science because they enable us to treat computation as data: a computable expression is encoded as a machine readable data structure that can be used as the input or output of another program. For instance, you could imagine a program that receives a computation graph and returns a new computation graph that implements a large-scale distributed version of the same computation - this would mean that you could distribute any computation without having to write the distribution logic yourself. Or imagine a program that automatically generates the derivative of the expression it represents. It’s much easier to do these things if your computation is expressed as an explicit graph data structure rather than as a series of Python statements.

To explain backpropagation clearly, let’s look at a really basic example of a computation graph in next figure. We will consider a simplified version of previous figure, where we have only one linear layer and where all variables are scalar. We will take two scalar variables w and b, a scalar input x, and apply some operations to them combine them into an output y. Finally, we will apply an absolute value error-loss function: loss_val = abs(y_true - y). Since we want to update w and b in a way that will minimize loss_val, we are interested in computing grad(loss_val, b) and grad(loss_val, w).

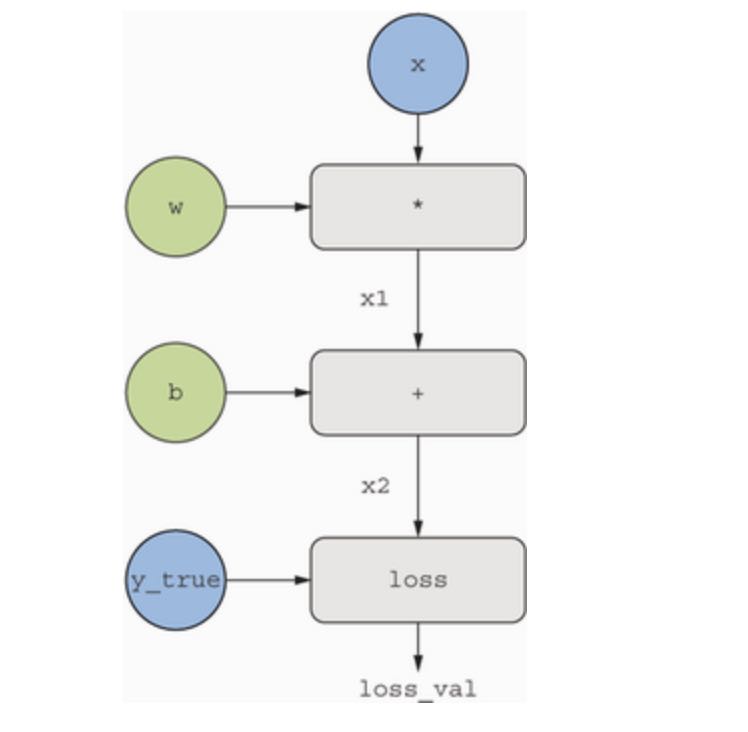
Let’s set concrete values for the “input nodes” in the graph, that is to say, the input x, the target y_true, the weight w, and the bias b. We will propagate these values to all nodes in the graph, from top to bottom, until we reach loss_val. This is the forward pass. See next figure:

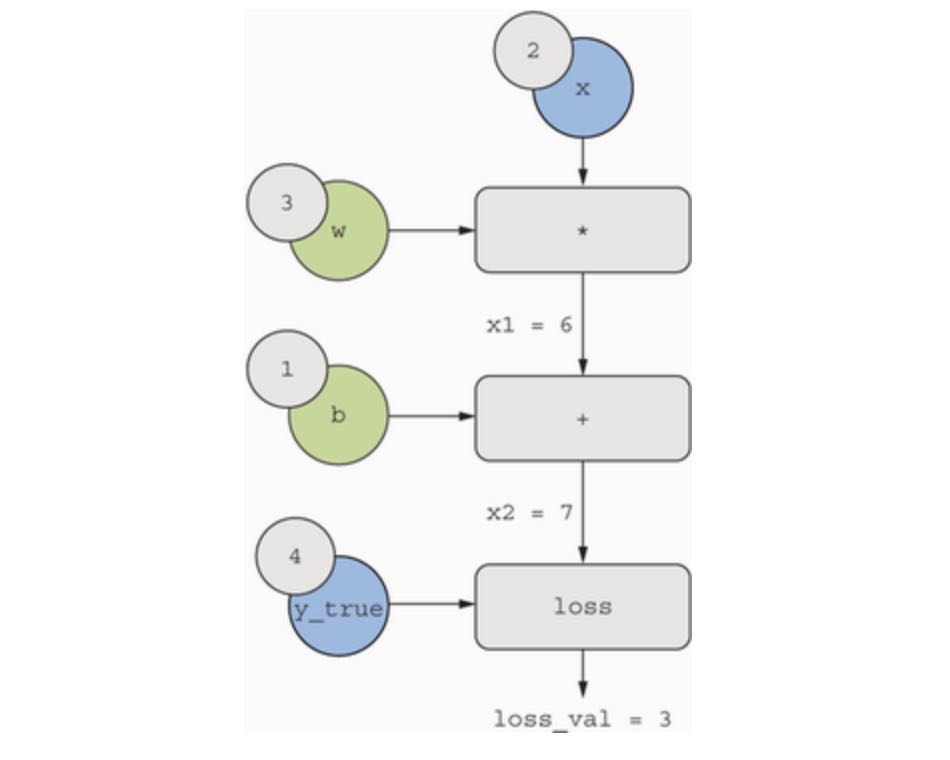
Now let’s “reverse” the graph: for each edge in the graph, going from A to B, we will create an opposite edge from B to A, and ask, how much does B vary when A varies? That is to say, what is grad(B, A)? We will annotate each inverted edge with this value. This backward graph represents the backward pass. See the following figure:

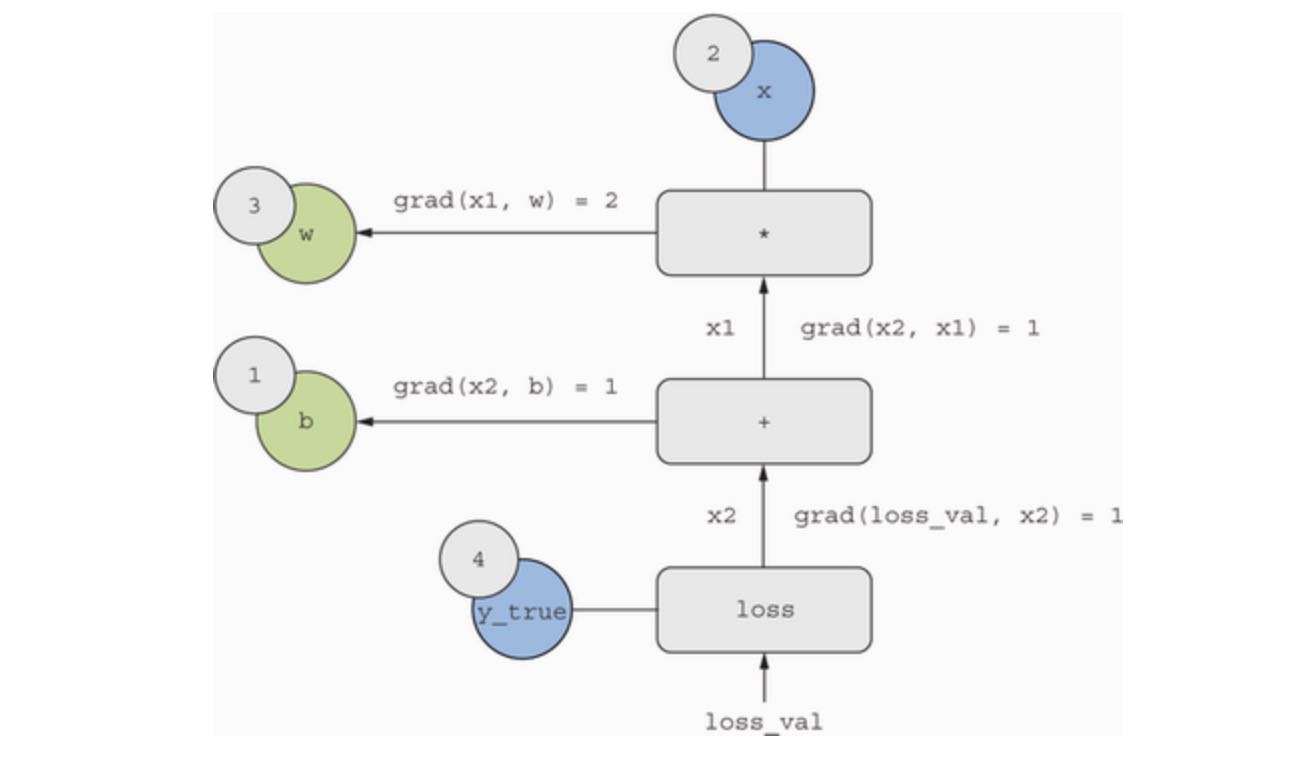
We have the following:

• grad(loss_val, x2) = 1, because as x2 varies by an amount epsilon, loss_val = abs(4-x2) varies by the same amount.
• grad(x2, x1) = 1, because as x1 varies by an amount epsilon, x2 = x1 + b = x1 + 1 varies by the same amount.
• grad(x2, b) = 1, because as b varies by an amount epsilon, x2 = x1 + b = 6 + b varies by the same amount.
• grad(x1, w) = 2, because as w varies by an amount epsilon, x1 = x * w = 2 * w varies by 2 times that amount.

What the chain rule says about this backward graph is that you can obtain the derivative of a node with respect to another node by multiplying the derivatives of each edge aloong the path inking the two nodes. For instance, grad(loss_val, w) = grad(loss_val, x2) * grad(x2, x1) * grad(x1, w). See the next figure:

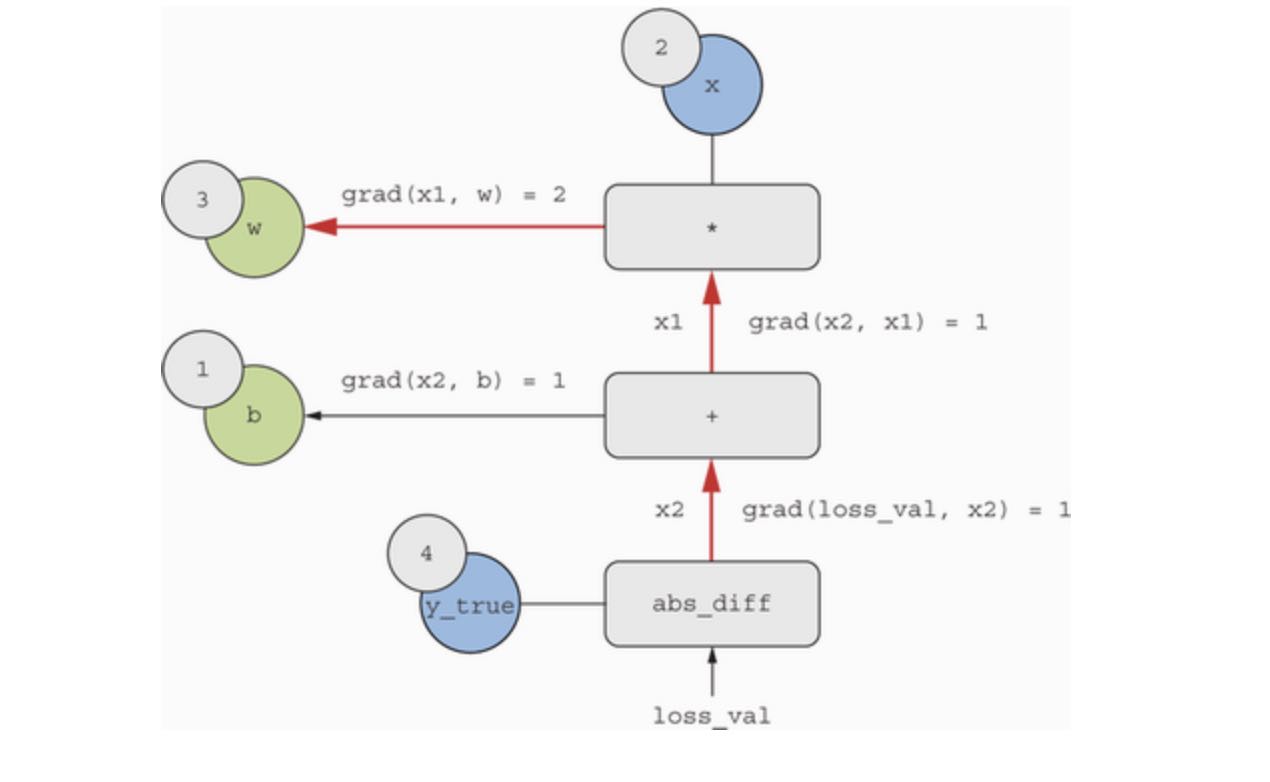
By applying chain rule to our graph, we obtain what we were looking for:

• grad(loss_val, w) = 1 * 1 * 2 = 2
• grad(loss_val, b) = 1 * 1 = 1

Note: If there are multiple paths linking the two nodes of interest, a and b, in the backward graph, we could obtain grad(b, a) by summing the contributions of all the paths.

And with that you just saw backpropagation in action! Backpropagation is simply application of the chain rule to a computation graph. There’s nothing more to it. Backpropagation starts with the final loss value and works backward from the top layers to the bottom layers, computing the contribution that each parameter had in the loss value. That’s where the name “backpropagation” comes from: we “back propagate” the loss contributions of different nodes in a computation graph.

Nowadays, people implement neural networks in modern frameworks that are capable of automatic differentiation, such as TensorFlow. Automatic differentiation is implemented with the kind of computation graph you have just seen. Automatic differentiation makes it possible to retrieve the gradients of arbitrary compositions of differentiable tensor operations without doing any extra work besides writing diwn the forward pass. When I wrote my first neural network in C in 2000s, I had to write my gradients by hand. Now, thanks to modern automatic differentiation tools, you will never have to implement backpropagation yourself. Consider yourself lucky!

THE GRADIENT TAPE IN TENSORFLOW:

The API through which you can leverage TensorFlow’s powerful automatic differentiation capabilities is the GradientTape. It’s a Python scope that will “record” the tensor operations that run inside it, in the form of a computation graph (sometimes called “tape”). This graph can then be used to retrieve the gradient of any output with respect to any variable or set of variables (instances of the tf.Variable class). A tf.Variable is a specific kind of tensor meant to hold mutable state - for instance, the weights of a neural network are always tf.Variable instances.

import tensorflow as tf
x = tf.Variable(0.0)  ## Instantiate a scalar Variable with an initial value of 0.0
with tf.GradientTape() as tape:  ## Open a GradientTape scope
    y = 2 * x + 3   ## Inside the scope apply some tensor operations to our variable
grad_of_y_wrt_x = tape.gradient(y, x)  ## Use the tape to retrieve the gradient of the output y with respect to our variable x

The GradientTape works with tensor operations:

x = tf.Variable(tf.random.uniform((2, 2)))  ## Instantiate a Variable with shape(2, 2) and an initial value of all zeros.

with tf.GradientTape() as tape:
    y = 2 * x + 3

grad_of_y_wrt_x = tape.gradient(y, x)  ## grad_of_t_wrt_x is a tensor of shape (2, 2) (like x) describing the curvature of y = 2*a + 3 around x = [[0,0], [0,0]]

It also works with a list of variables:

W = tf.Variable(tf.random.uniform((2, 2)))
b = tf.Variable(tf.zeros((2, )))
x = tf.random.uniform((2, 2))
with tf.GradientTape() as tape:
    y = tf.matmul(x, W) + b  ## matmul is how you say "dot product" in TensorFlow
grad_of_y_wrt_W_and_b = tape.gradient(y, [W, b])  ## grad_of_y_wrt_W_and_b is a list of two tensors with the same shape as W and b, respectively

You will learn about the gradient tape in the next chapter.

2.5 Looking back at our first example

You’re nearing the end of this chapter, and should now have a general understanding of what’s going on behind the scenes in a neural network. What was magical black box at the start of the chapter has turned into a clear picture, as illustrated in the following figure:

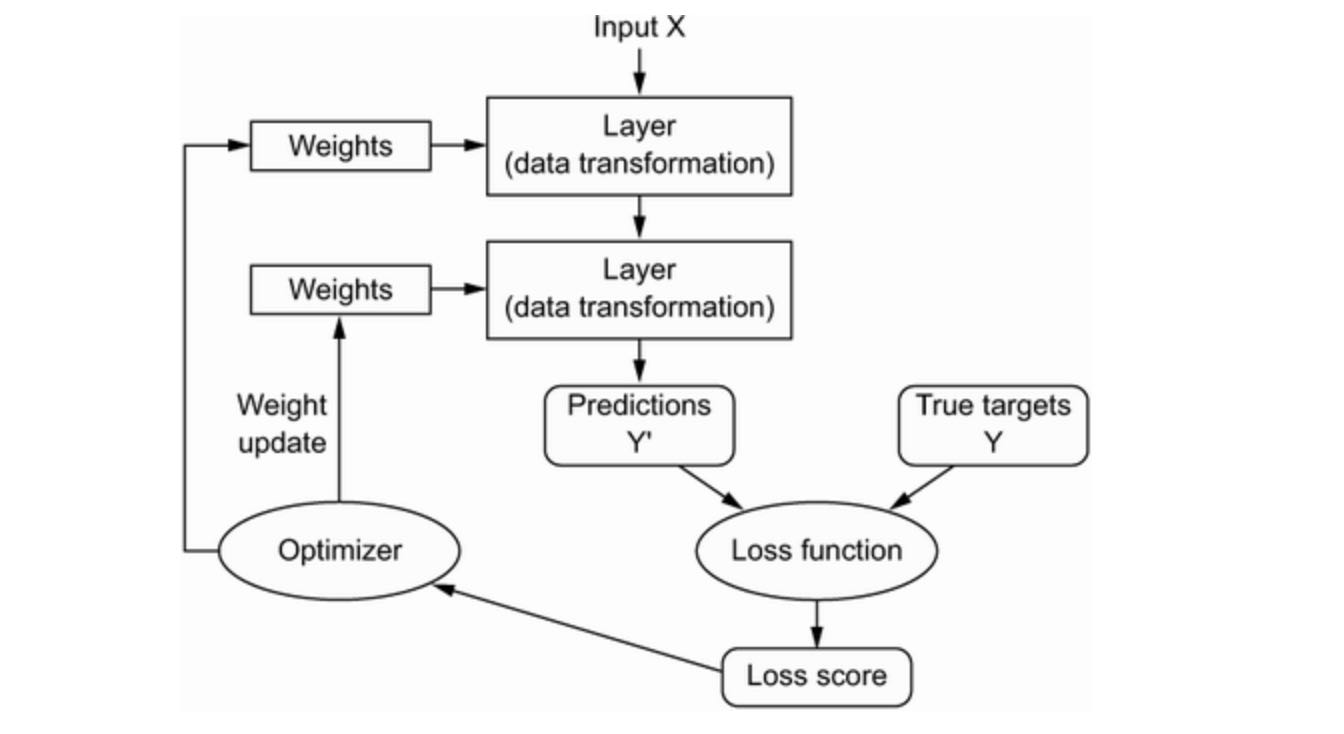
The picutre describes the relationship between the network, layers, loss function and optimizer. Here, the model, composed of layers that are chained together, maps the input data to predictions. The loss function then compares these predections to the targets, producing a loss value: a measure of how well the model’s predictions match what was expected. The optimizer uses this loss value to update the model’s weights.

Let’s go back to the first example in this chapter and review each piece of it in the light of what you’ve learned since.

This was the input data:

(train_images, train_labels), (test_images, test_labels) = tf.keras.datasets.mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

Now you understand that the input images are stored in NumPy tensors, which are here formatted as float32 tensors of shape (60000, 784) and (10000, 784) respectively.

This was our model:

model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(512, activation='relu'),
    tf.keras.layers.Dense(10, activation='softmax')
])

Now you understand that this model consists of a chain of two Dense layers, that each layer applies a few simple tensor operations to the input data, and that these operations involve weight tensors. Weight tensors, which are attributes of the layers, are where the knowledge of the model persists.

This was the mode-compilation step:

model.compile(optimizer='rmsprop',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

Now you understand that sparse_categorical_crossentropy is the loss function that’s used as a feedback signal for learning the weight tensors, and which the training phase will attempt to minimize. You also know that this reduction of the loss happens via mini-batch stochastic gradient descent. The exact rules governing a specific use of gradient descent are defined by the rmsprop optimizer passed as the first argument.

Finally, this was the training loop:

model.fit(train_images, train_labels, epochs=5, batch_size=128)

Now you understnd what happens when you call fit: the model will start to iterate on the training data in mini-batches of 128 samples, 5 times over (each iteration over all the training data is called an epoch). For each batch, the model will compute the gradient of the loss with regard to weights (using the Backpropagation algorithm which derives from the chain rule in calculus) and move the weights in the direction that will reduce the value of the loss for this batch.

After these 5 epochs, the model will have performed 2,345 gradient updates(469 per epoch)(how??), and the loss of the model will be sufficiently low that the model will be capable of classifying handwritten digits with high accuracy.

At this point, you already know most of what there is to know about neural networks. Let’s prove it by reimplementing a simplified version of that first example from scratch, in TensorFlow, step by step.

2.5.1 Reimplementing our first example from scratch in TensorFlow

What better demonstrates full, unambiguous understanding than implementing everything from scratch? Of course, what “from scratch” means here is relative: we wouldn’t reimplement basic tensor operations, and we wouldn’t reimplement backpropagation. But we’ll go to such a low level that we will barely use any Keras functionality at all.

Don’t worry if you don’t understand every little detail in this example just yet. The next chapter will dive in more detail into TensorFlow API. For now, just try to follow the gist of what’s going on - the intent of this example is to help crystalize your understanding of the mathematics of deep learning using concrete implementation. Let’s go!

A SIMPLE DENSE CLASS:

You’ve learned earlier that the Dense layer implements the following input transoformation, where W and b are model parameters, and activation is an element-wise function(usually relu, but it would be softmax for the last layer):

output = activation(dot(W, input) + b)

Let’s implement a simple Python class, NaiveDense, that creates two TensorFlow variables, W and b, and exposes a __call__() method that applies the preceding transformation:

import tensorflow as tf

class NaiveDense:
    def __init__(self, input_size, output_size, activation):
        self.activation = activation

        w_shape = (input_size, output_size)  ## Create a matrix, W, of shape (input_size, output_size), initialized with random values
        w_initial_value = tf.random.uniform(w_shape, minval=0, maxval=1e-1)
        self.W = tf.Variable(w_initial_value)

        b_shape = (output_size,)  ## Create a vector, b, of shape (output_size,), initialized with zeros
        b_initial_value = tf.zeros(b_shape)
        self.b = tf.Variable(b_initial_value)

    def __call__(self, inputs):  ## Apply a forward pass
        return self.activation(tf.matmul(inputs, self.W) + self.b)

    @property
    def weights(self):  ## Convenience method for retrieving the layer's weights
        return [self.W, self.b]

A SIMPLE SEQUENTIAL CLASS:

Now, let’s create a NaiveSequential class to chain these layers. It wraps a list of layers and exposes a __call__() method that simply calls the underlying layers on the inputs, in order. It also feature a weights property to easily keep track of the layers’ parameters.

class NaiveSequential:
    def __init__(self, layers):
        self.layers = layers

    def __call__(self, inputs):
        x = inputs
        for layer in self.layers:
            x = layer(x)
        return x

    @property
    def weights(self):
        weights = []
        for layer in self.layers:
            weights += layer.weights
        return weights

Using the NaiveDense class and this NaiveSequential class, we can create a mock Keras model:

model = NaiveSequential([
    NaiveDense(input_size=28 * 28, output_size=512, activation=tf.nn.relu),
    NaiveDense(input_size=512, output_size=10, activation=tf.nn.softmax)
])
assert len(model.weights) == 4

A BATCH GENERATOR

Next, we need a way to iterate over the MNIST data in mini-batches. This is easy:

import math

class BatchGenerator:
    def __init__(self, images, labels, batch_size=128):
        self.index = 0
        self.images = images
        self.labels = labels
        self.batch_size = batch_size
        self.num_batches = math.ceil(len(images) / batch_size)

    def next(self):
        images = self.images[self.index: self.index + self.batch_size]
        labels = self.labels[self.index: self.index + self.batch_size]
        self.index += self.batch_size
        return images, labels

2.5.2 Running one training step

The most difficult part of the process is the “training step”: updating the weights of the model after running it on one batch of data. We need to:

1. Compute the predictions of the model for the images in the batch.
2. Compute the loss value for these predictions, given the actual labels.
3. Compute the gradient of the loss with regard to the model’s weights.
4. Move the weights by a small amount in the direction opposite to the gradient.

To compute the gradient, we will use the TensorFlow GradientTape class.

def one_training_step(model, images_batch, labels_batch):
    with tf.GradientTape() as tape:  ## Run the "forward pass"(compute the model's predictions under a GradientTape scope)
        predictions = model(images_batch)
        per_sample_losses = tf.keras.losses.sparse_categorical_crossentropy(labels_batch, predictions)
        average_loss = tf.reduce_mean(per_sample_losses)
    gradients = tape.gradient(average_loss, model.weights)  ## Compute the gradient of the loss with regard to the weights. The output gradients is a list where each entry corresponds to a weight from the model.weights list.
    update_weights(gradients, model.weights)  ## Update the weights using the gradients (we will define this function shortly)
    return average_loss

As you already know, the purpose of the “weight update” step (represented by the preceding update_weights function) is to move the weights by “a bit” in a direction that will reduce the loss on this batch. The magnitude of the move is determined by the “learning rate” parameter, typically a small quantity. The simplest way to implement this update_weights function is to subtract the gradient * learning_rate from each weight:

learning_rate = 1e-3

def update_weights(gradients, weights):
    for g, w in zip(gradients, weights):
        w.assign_sub(g * learning_rate)  ## assign_sub is the equivalent of -= for TensorFlow Variables

In practice, you would almost never implement a weight update step like this by hand. Instead, you would use an Optimizer instance from Keras, like this:

from tensorflow.keras import optimizers

optimizer = optimizers.SGD(learning_rate=1e-3)

def update_weights(gradients, weights):
    optimizer.apply_gradients(zip(gradients, weights))

Now that our per-batch training step is ready, we can move on to implementing an entire epoch of training.

2.5.3 The full training loop

An epoch of training simply consists of repeating the training step for each batch in the training data, and the full training loop is simply the repetition of one epoch:

def fit(model, images, labels, epochs, batch_size=128):
    for epoch_counter in range(epochs):
        print(f"Epoch {epoch_counter}")
        batch_generator = BatchGenerator(images, labels)
        for batch_counter in range(batch_generator.num_batches):
            images_batch, labels_batch = batch_generator.next()
            loss = one_training_step(model, images_batch, labels_batch)
            if batch_counter % 100 == 0:
                print(f"loss at batch {batch_counter}: {loss:.2f}")

Let’s test drive it:

from tensorflow.keras.datasets import mnist

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

fit(model, train_images, train_labels, epochs=5, batch_size=128)

2.5.4 Evaluating the model

We can evaluate the model by taking the argmax of its predictions over the test images and comparing it to the expected labels:

predictions = model(test_images)
predictions = predictions.numpy()  ## Calling .numpy() on a TensorFlow tensor converts it to a NumPy tensor.
predicted_labels = np.argmax(predictions, axis=1)
matches = predicted_labels == test_labels
print(f"accuracy: {matches.mean():.2f}")

All Done! As you can see, it’s quite a bit of work to do “by hand” what you can do in a few lines of Keras code. But because you’ve gone through the steps, you should now have a crystal clear understanding of what goes inside a neural network when you call fit(). Having this low-level mental model of what you code is doing behind the scenes will make you better able to leverage the high-level feature of the Keras API.

SUMMARY:

• Tensors form the foundation of modern machine learning systems. They come in various flavours of dtype, rank, and shape.
• You can manipulate numerical tensors via tensor operations (such as addition, tensor product, or element-wise multiplication), which can be interpreted as encoding geometric transformations. In general, everything in deep learning is amenable to geometric interpretation.
• Deep learning models consist of chains of simple tensors operations, parameterized by weights, which are themselves tensors. The weights of a model are where its “knowledge” is stored.
• Learning means finding a set of values for the model’s weights that minimizes a loss function for a given set of training data samples and their corresponding targets.
• Learning happens by drawing random batches of data samples and their targets, and computing the gradient of the model parameters with respect to the loss on the batch. The model parameters are then moved a bit (the magnitude of the move is defined by the learning rate) in the opposite direction from the gradient. This is called mini-batch stochastic gradient descent.
• The entire learning process is made possible by the fact that all tensor operations in neural networks are differentiable, and thus it’s possible to apply the chain rule of derivation to find the gradient function mapping the current parameters and current batch of data to a gradient value. This is called Backpropagation.
• Two key concepts you will see frequently in future chapters are loss and optimizers. These are the two things you need to define before you begin feeding data into a model.
• • The loss is the quantity you will attempt to minimize during training, so it should represent a measure of success for the task you’re trying to solve.
• • The optimizer specifies the exact way in which the gradient of the loss will be used to update parameters: for instance, it could be the RMSProp optimizer, SGD with momentum, and so on.

Previous Chapter: Deep Learning Chapter 1 Summary

Next Chapter: Deep Learning Chapter 3 Summary